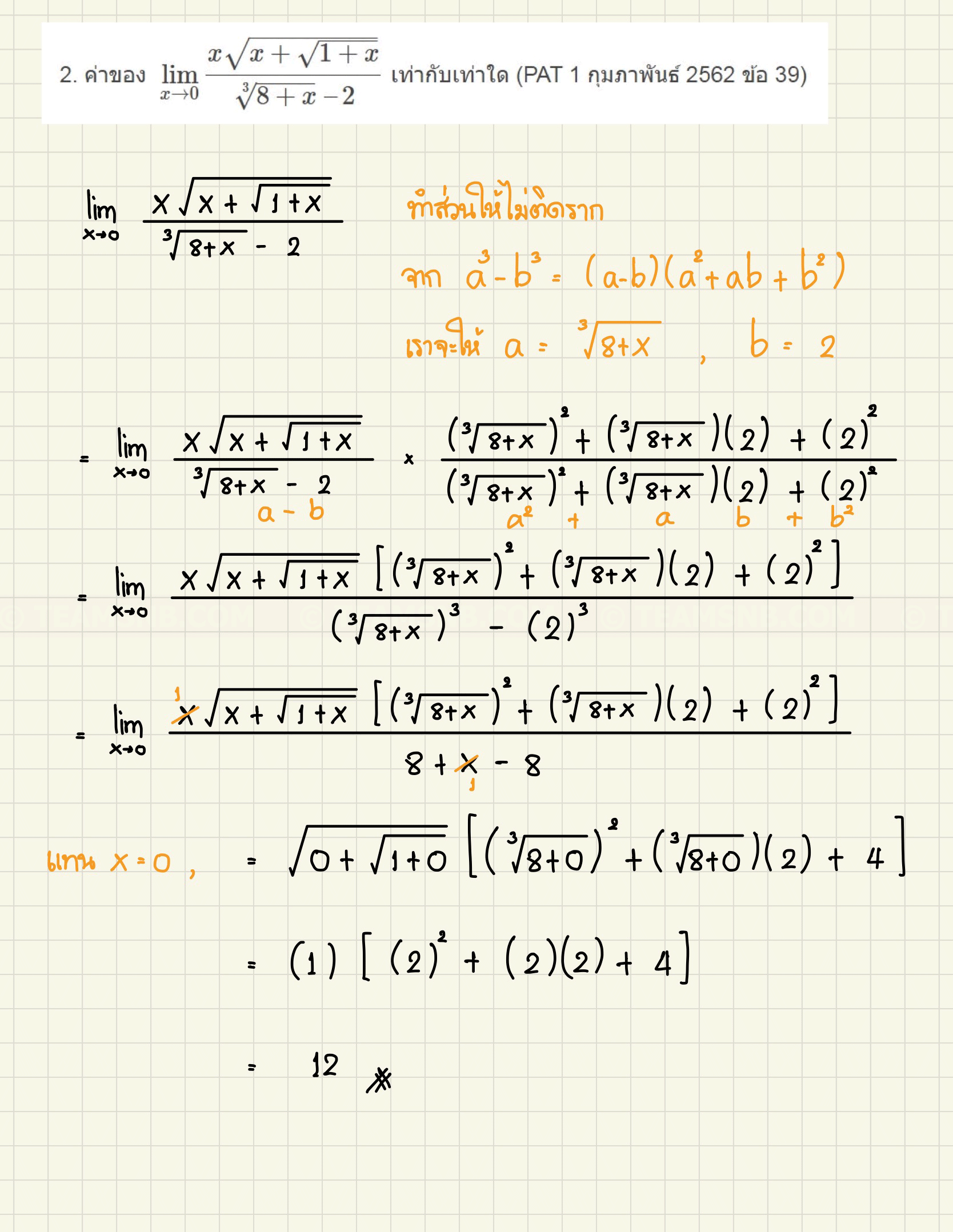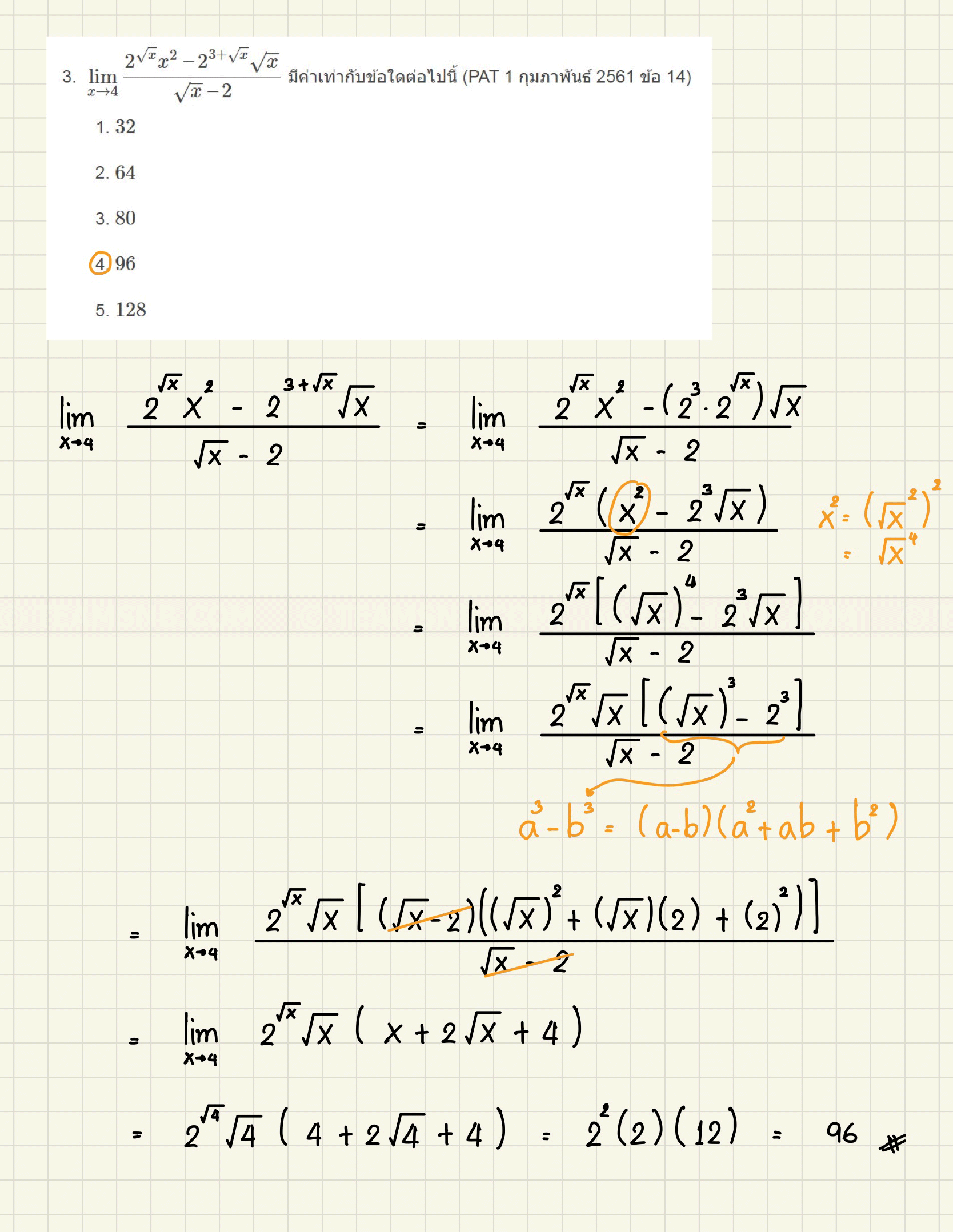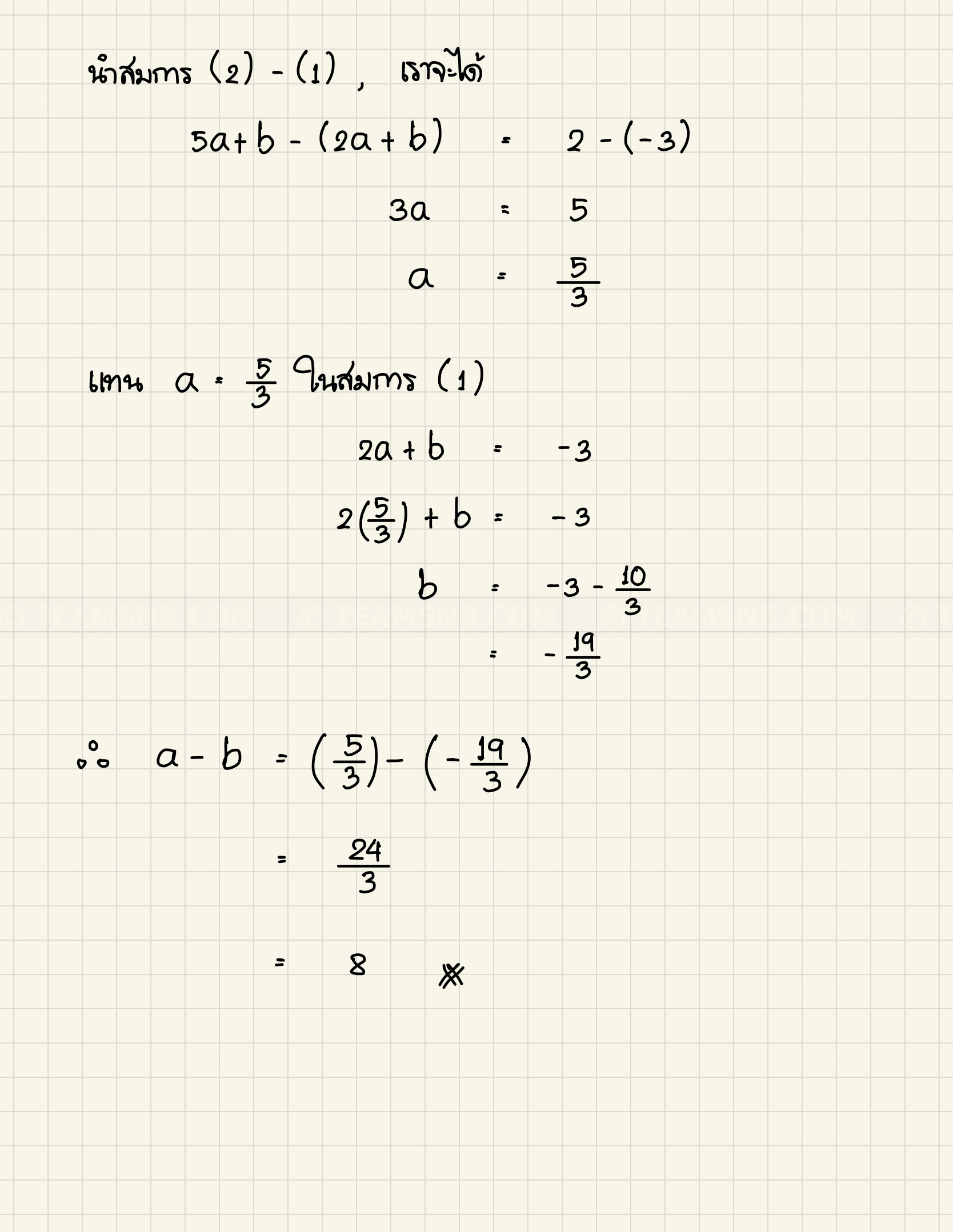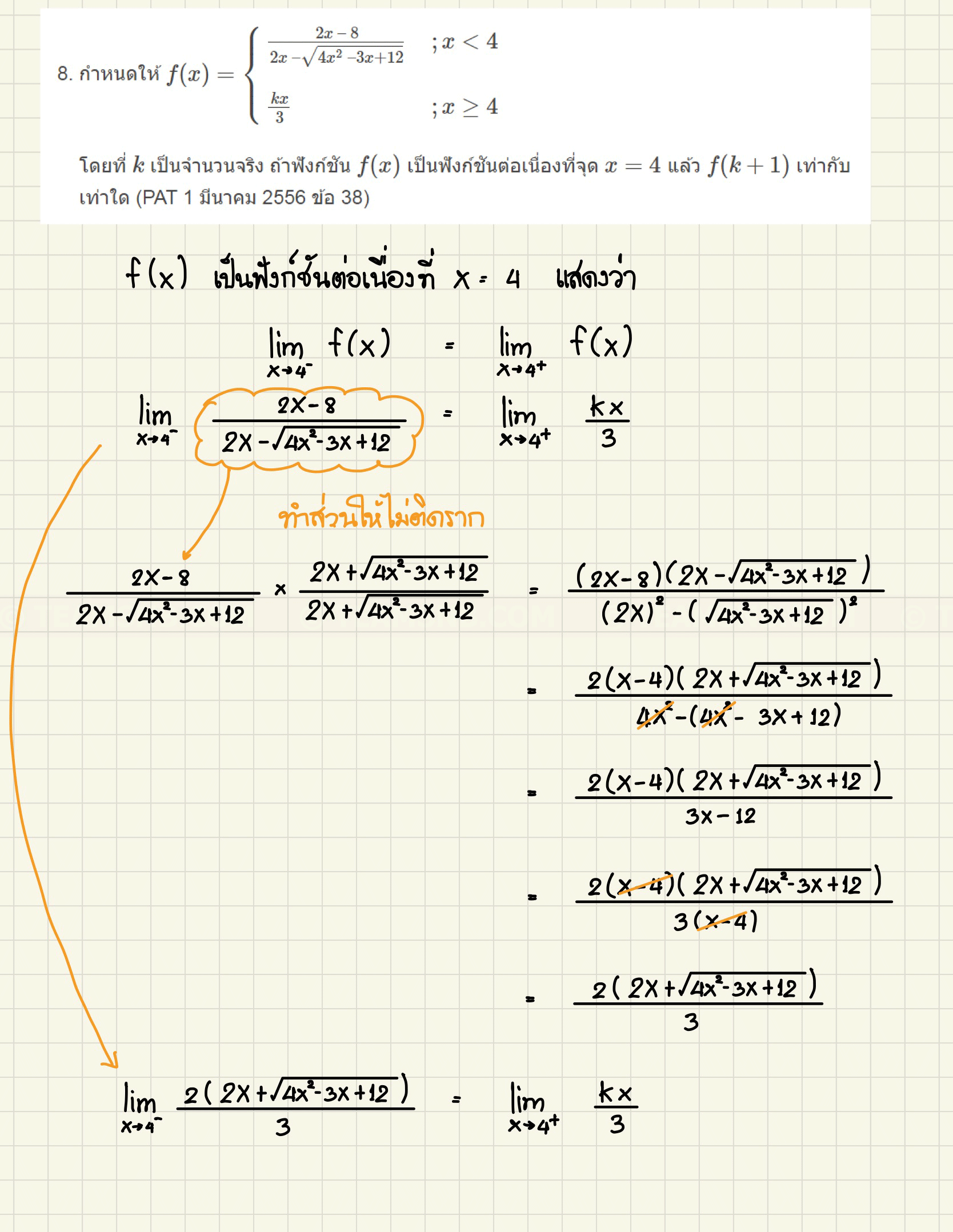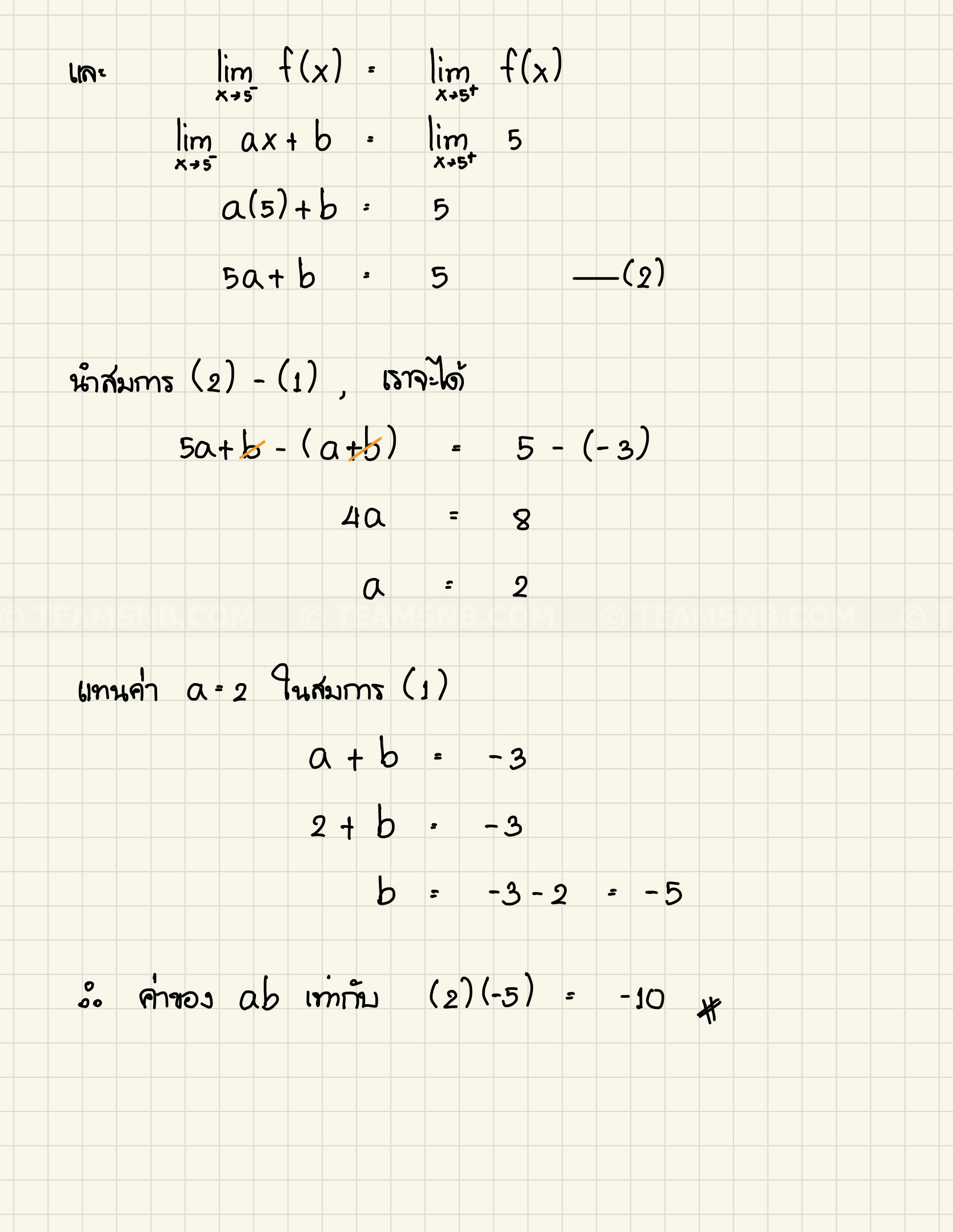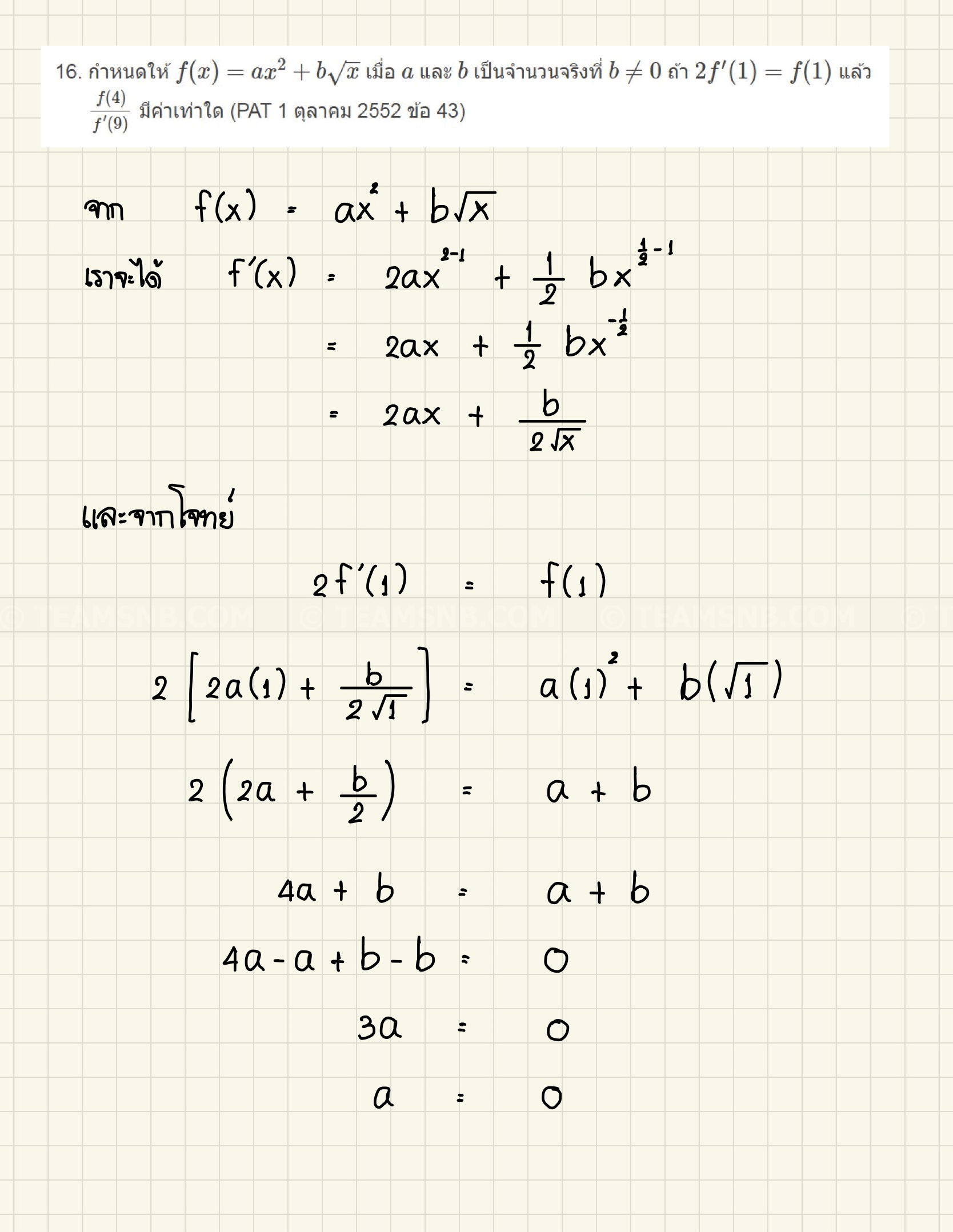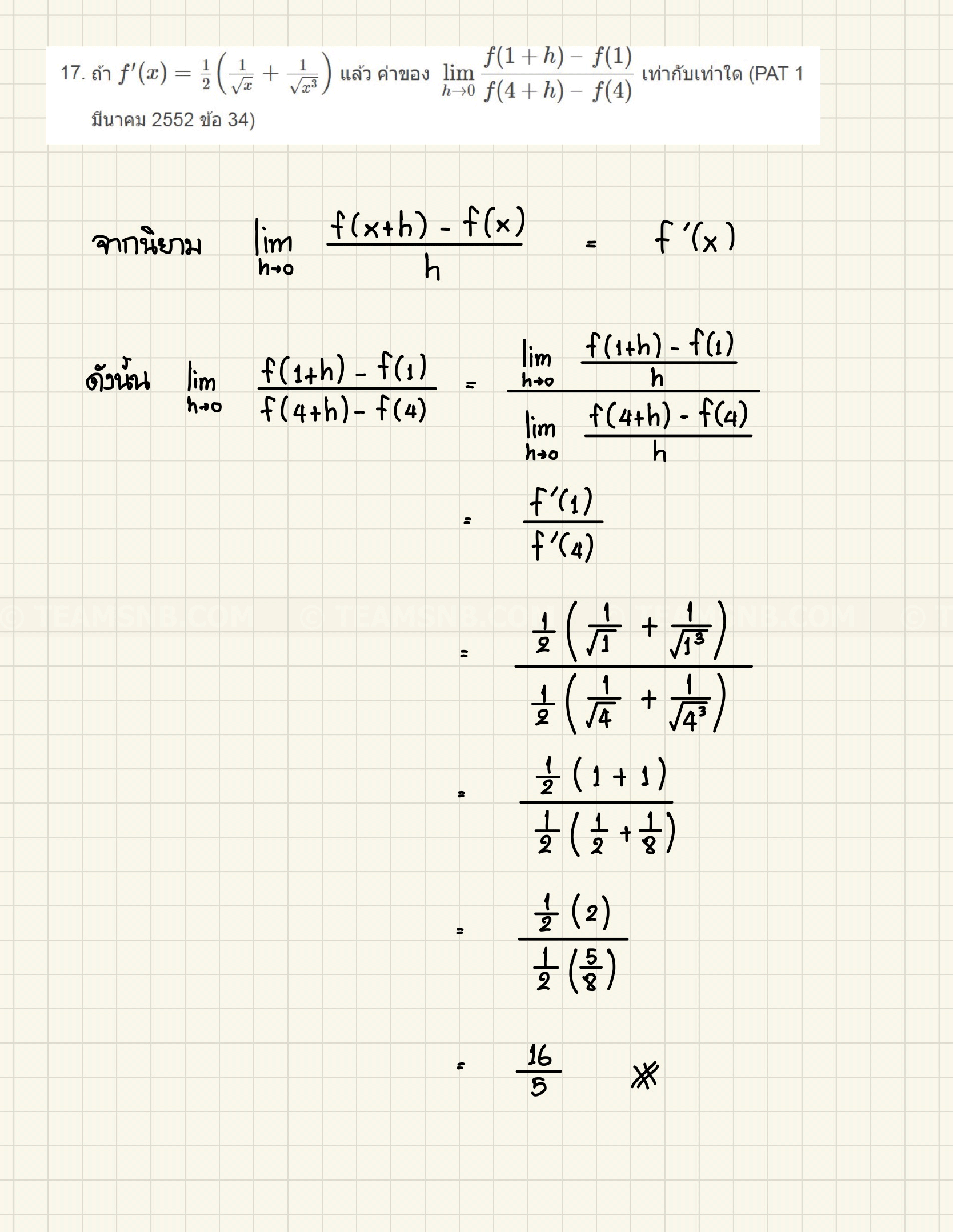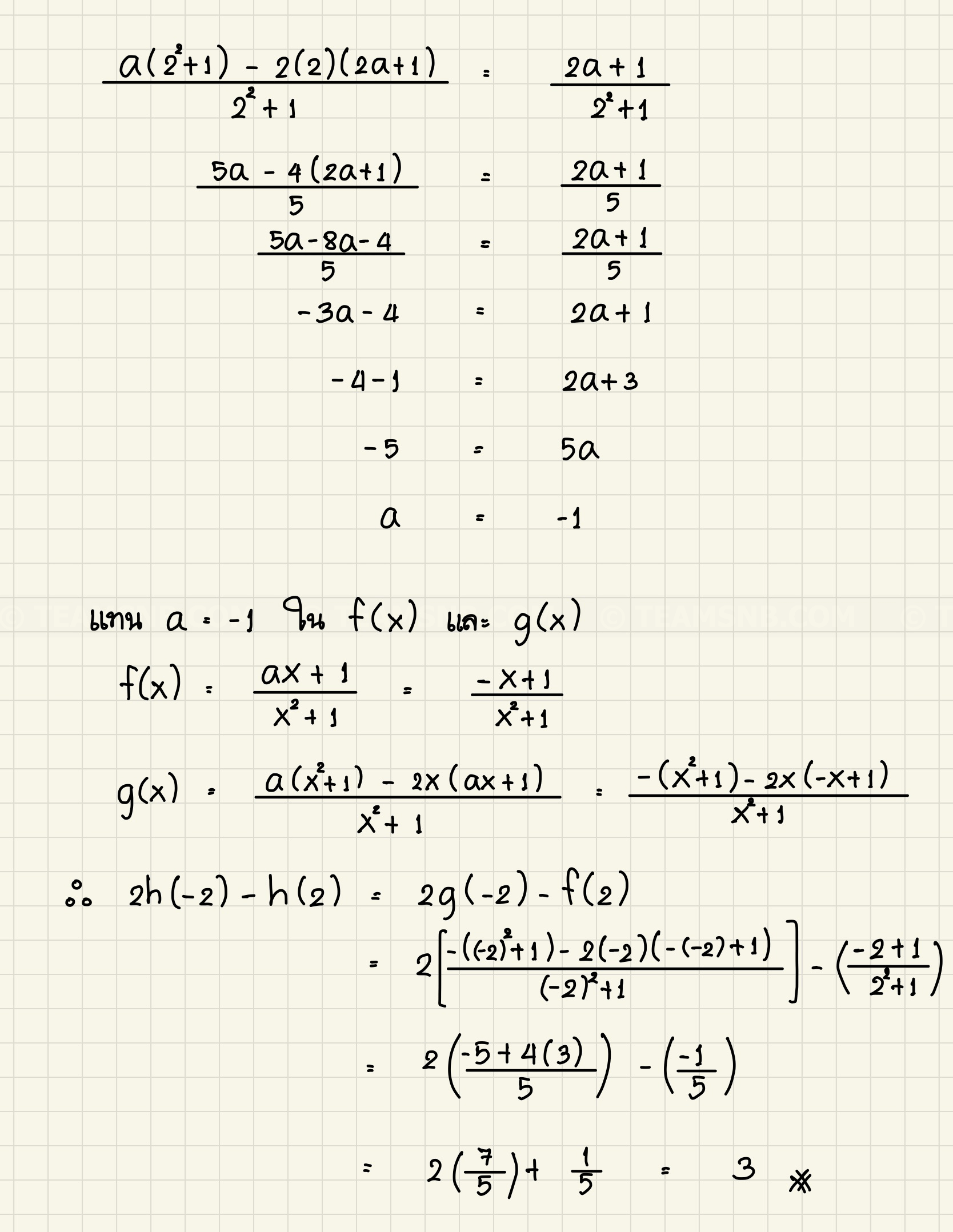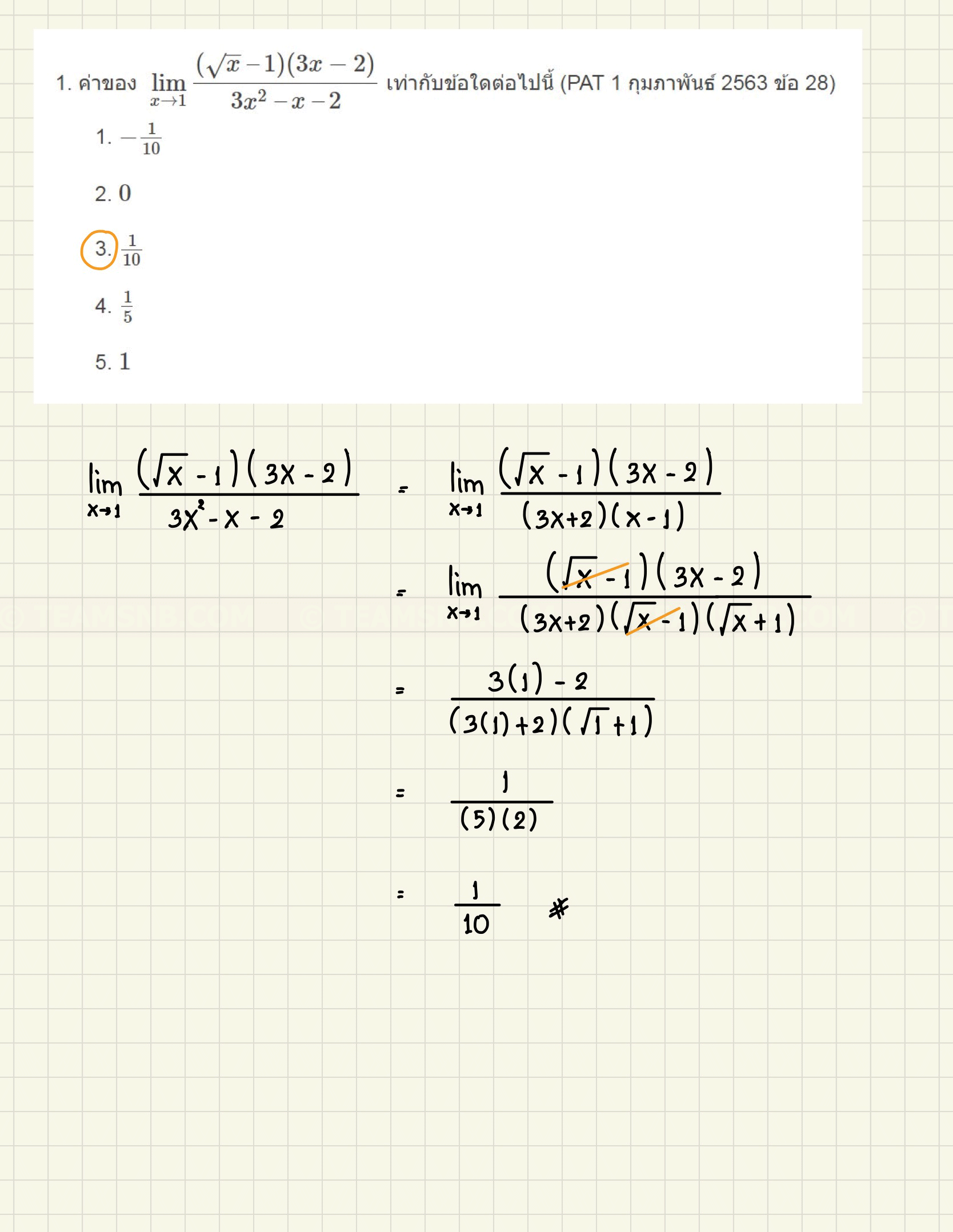
- ค่าของ \(\displaystyle \; \lim_{x\rightarrow 1} \frac{(\sqrt{x} \ – 1)(3x-2)}{3x^2 \ – x \ – 2}\) เท่ากับข้อใดต่อไปนี้ (PAT 1 กุมภาพันธ์ 2563 ข้อ 28)
- \( -\frac{1}{10} \)
- \( 0 \)
- \( \frac{1}{10} \)
- \( \frac{1}{5} \)
- \( 1 \)
- ค่าของ \(\displaystyle \; \lim_{x\rightarrow 0} \frac{x \sqrt{x + \sqrt{1 + x}}}{\sqrt[3] {8 + x} \ – 2}\) เท่ากับเท่าใด (PAT 1 กุมภาพันธ์ 2562 ข้อ 39)
- \(\displaystyle \; \lim_{x\rightarrow 4} \frac{2^{\sqrt{x}} x^2 \ – 2^{3 + \sqrt{x}} \sqrt{x}}{\sqrt{x} \ – 2}\) มีค่าเท่ากับข้อใดต่อไปนี้ (PAT 1 กุมภาพันธ์ 2561 ข้อ 14)
- \( 32 \)
- \( 64 \)
- \( 80 \)
- \( 96 \)
- \( 128 \)
- ค่าของ \(\displaystyle \; \lim_{x\rightarrow 3} \frac{3^{x} x \ – 3^{x + 1}}{\sqrt[3]{x \ – 2} \ – 1}\) เท่ากับเท่าใด (PAT 1 มีนาคม 2560 ข้อ 38)
- กำหนดให้ \(a\) เป็นจำนวนจริงบวก สอดคล้องกับ \(\displaystyle \; \lim_{x\rightarrow 0} \frac{|5x + 1| \ – |5x \ – 1|}{\sqrt{x + a} \ – \sqrt{a}} = 80\) แล้ว ค่าของ \(a^2 + a + 58\) เท่ากับข้อใดต่อไปนี้ (PAT 1 มีนาคม 2558 ข้อ 17)
- \( 64 \)
- \( 78 \)
- \( 130 \)
- \( 330 \)
- กำหนดให้ \(f\) เป็นฟังก์ชันนิยามโดย \(f(x) =
\begin{cases}
x^2 + ax + b &; x \lt 2 \\[2ex] \sqrt{x \ – 1} &; 2 \leq x \leq 5 \\[2ex] ax + b &; x \gt 5
\end{cases} \) โดยที่ \(a\) และ \(b\) เป็นจำนวนจริง ถ้า \(f(x)\) เป็นฟังก์ชันต่อเนื่องบนเซตของจำนวนจริง แล้ว \(a \ – b\) เท่ากับข้อใดต่อไปนี้ (PAT 1 มีนาคม 2557 ข้อ 17)- \( 5 \)
- \( 8 \)
- \( 11 \)
- \( 12 \)
- กำหนดให้ \(f\) เป็นฟังก์ชันนิยามโดย \(f(x) =
\begin{cases}
-x + a &; x \leq -2 \\[2ex] -\frac{2}{5}x + b &; -2 \lt x \lt 3 \\[2ex] x^2 \ – 6x + 11 &; x \gt 3
\end{cases} \) เมื่อ \(a\) และ \(b\) เป็นจำนวนจริง ถ้าฟังก์ชัน \(f\) มีความต่อเนื่องที่ \(x = -2\) และ \(\displaystyle \; \lim_{x\rightarrow 3} f(x)\) หาค่าได้ แล้ว \(|a + 5b|\) เท่ากับข้อใดต่อไปนี้ (PAT 1 เมษายน 2557 ข้อ 17)- \( 8 \)
- \( 18 \)
- \( \frac{88}{5} \)
- \( \frac{102}{5} \)
- กำหนดให้ \(f(x) =
\begin{cases}
\frac{2x \ – \ 8}{2x \ – \sqrt{4x^2 \ – 3x + 12}} &; x \lt 4 \\[2ex] \frac{kx}{3} &; x \geq 4
\end{cases} \) โดยที่ \(k\) เป็นจำนวนจริง ถ้าฟังก์ชัน \(f(x)\) เป็นฟังก์ชันต่อเนื่องที่จุด \(x = 4\) แล้ว \(f(k + 1)\) เท่ากับเท่าใด (PAT 1 มีนาคม 2556 ข้อ 38) - กำหนดให้ \(f(x) =
\begin{cases}
\frac{x \ – \ 3}{\sqrt{2x + 10} \ – \sqrt{x + 13}} &; x \neq 3 \\[2ex] a &; x = 3
\end{cases} \) โดยที่ \(a\) เป็นจำนวนจริง ถ้า \(f(x)\) เป็นฟังก์ชันต่อเนื่องที่จุด \(x = 3\) แล้ว \(a\) เท่ากับเท่าใด (PAT 1 มีนาคม 2554 ข้อ 44) - กำหนดให้ \(R\) แทนเซตของจำนวนจริง ให้ \(f: R \to R\) เป็นฟังก์ชันต่อเนื่องที่ \(x = 1\) และให้ \(g\) เป็นฟังก์ชันที่กำหนดโดย \(g(x) =
\begin{cases}
\frac{\sqrt{x + 3} \ – \ 2}{\sqrt{x} \ – \ 1} &; x \gt 1 \\[2ex] \frac{f(x)}{|x| + 7} &; x \leq 1
\end{cases} \) ถ้าฟังก์ชัน \(g\) มีความต่อเนื่องที่จุด \(x = 1\) แล้ว ค่าของ\((g \circ f)(1)\) เท่ากับข้อใดต่อไปนี้ (PAT 1 ตุลาคม 2553 ข้อ 18)- \( 2 \ – \sqrt{3} \)
- \( 2 \)
- \( 2 \ – \sqrt{7} \)
- \( \sqrt{7} \ – 2 \)
- กำหนดให้ \(a\) และ \(b\) เป็นจำนวนจริง และให้ \(f\) เป็นฟังก์ชัน โดยที่ \(f(x) =
\begin{cases}
\frac{|x^3 \ – \ 1|}{x \ – \ 1} &; -1 \lt x \lt 1 \\[2ex] ax + b &; 1 \leq x \lt 5 \\[2ex] 5 &; x \geq 5
\end{cases} \) ถ้า \(f\) เป็นฟังก์ชันต่อเนื่องบนช่วง \((-1, \infty)\) แล้ว ค่าของ \(ab\) เท่ากับข้อใดต่อไปนี้ (PAT 1 กรกฎาคม 2553 ข้อ 19)- \( \frac{5}{4} \)
- \( -\frac{7}{4} \)
- \( 15 \)
- \( -10 \)
- กำหนดให้ \(a\) เป็นจำนวนจริง และ
\(f(x) =
\begin{cases}
x + \sqrt{x^2 + 5} &; x \geq a \\[2ex] \frac{15}{\sqrt{x^2 + 5}} &; x \lt a
\end{cases} \) ถ้าฟังก์ชัน \(f\) มีความต่อเนื่องทุกจำนวนจริง \(x\) แล้ว ค่าของ \(f(a) + f(-a)\) เท่ากับเท่าใด (PAT 1 มีนาคม 2560 ข้อ 41) - กำหนดให้ \(a\) และ \(b\) เป็นจำนวนจริง และให้ \(f\) เป็นฟังก์ชัน ซึ่งนิยามโดย
\(f(x) =
\begin{cases}
\frac{x}{x \ – \ x^2} &; x \lt 0 \\[2ex] \frac{ax^2 + (b \ – \ a)x \ – \ b}{x \ – \ 1} &; 0 \leq x \lt 1 \\[2ex] (x + b)^2 &; x \geq 1
\end{cases} \) ถ้า \(f\) เป็นฟังก์ชันต่อเนื่องบนเซตของจำนวนจริงแล้ว ค่าของ \(f(a + b)\) เท่ากับข้อใดต่อไปนี้ (PAT 1 กุมภาพันธ์ 2563 ข้อ 34)- \( 25 \)
- \( 16 \)
- \( 9 \)
- \( 4 \)
- \( \frac{1}{6} \)
- กำหนดให้ \(f\) เป็นฟังก์ชัน
โดยที่ \(f(x) =
\begin{cases}
\frac{3 \ – \ |x|}{3 \ – \ x} &; x \lt 3 \\[2ex] ax + 10 &; x \geq 3
\end{cases} \) เมื่อ \(a\) เป็นจำนวนจริง ถ้า \(f\) เป็นฟังก์ชันต่อเนื่องบนเซตของจำนวนจริงแล้ว ค่าของ \(f(a \ – 6) + f(a) + f(a + 6)\) เท่ากับเท่าใด (PAT 1 กุมภาพันธ์ 2561 ข้อ 35) - ถ้า \(f,g\) และ \(h\) สอดคล้องกับ
\(f(1) = g(1) = h(1) = 1\) และ
\(f'(1) = g'(1) = h'(1) = 2\) แล้ว
ค่าของ \((fg + h)'(1)\) เท่ากับเท่าไร (PAT 1 กรกฎาคม 2552 ข้อ 33)- \( 1 \)
- \( 2 \)
- \( 4 \)
- \( 6 \)
- กำหนดให้ \(f(x) = ax^2 + b\sqrt{x}\) เมื่อ \(a\) และ \(b\) เป็นจำนวนจริงที่ \(b \neq 0\) ถ้า \(2f'(1) = f(1)\) แล้ว \(\frac{f(4)}{f'(9)}\) มีค่าเท่าใด (PAT 1 ตุลาคม 2552 ข้อ 43)
- ถ้า \(f'(x) = \frac{1}{2}\left(\frac{1}{\sqrt{x}} + \frac{1}{\sqrt{x^3}}\right)\) แล้ว ค่าของ \(\displaystyle \; \lim_{h\rightarrow 0} \frac{f(1 + h) \ – \ f(1)}{f(4 + h) \ – \ f(4)}\) เท่ากับเท่าใด (PAT 1 มีนาคม 2552 ข้อ 34)
- กำหนดให้ \(R\) แทน เซตของจำนวนจริง ถ้า \(f: R \to R\) และ \(g: R \to R\) เป็นฟังก์ชันที่หาอนุพันธ์ได้ทุก \(x \in R\) โดยที่ \(g(x) = x^2 \ – 2x + 5\) และ \((g \circ f)(x) = x^6 + 2x^4 \ – 2x^3 + x^2 \ – 2x + 5\) และ \(f(0) = 0\) ค่าของ \((f’ \circ g’)(1) + (g’ \circ f’)(0)\) เท่ากับเท่าใด (PAT 1 มีนาคม 2554 ข้อ 42)
- ให้ \(R\) แทน เซตของจำนวนจริง ให้ \(f: R \to R\), \(g: R \to R\) และ \(h: R \to R\) เป็นฟังก์ชัน โดยที่ \(f(x) = \frac{ax + 1}{x^2 + 1}\) เมื่อ \(a\) เป็นจำนวนจริง
\(g(x) = (x^2 + 1)f'(x)\) และ \(h(x) =
\begin{cases}
f(x) &; x \geq2 \\[2ex] g(x) &; x \lt 2
\end{cases} \) ถ้าฟังก์ชัน \(h\) ต่อเนื่องที่ \(x = 2\) แล้ว ค่าของ \(2h(-2) \ – h(2)\) เท่ากับเท่าใด (PAT 1 มีนาคม 2555 ข้อ 17) - ให้ \(R\) แทน เซตของจำนวนจริง ให้ \(f: R \to R\) และ \(g: R \to R\) เป็นฟังก์ชัน โดยที่
\(f(x) = 3x^{\frac{2}{3}}\),
\(g(1) = 8\) และ \(g'(1) = \frac{2}{3}\) ค่าของ \((f \circ g)'(1)\) เท่ากับเท่าใด (PAT 1 มีนาคม 2553 ข้อ 18)
ดูเฉลยคำตอบ
