ให้นักเรียนเลือกคำตอบที่ถูกที่สุดเพียงคำตอบเดียว
- ข้อใดเป็นเซตของจำนวนเต็มที่มากกว่า \(100\)
- \(\{100, 101, 102, \ldots\}\)
- \(\{101, 102, 103, \ldots\}\)
- \(\{102, 103, 104, \ldots\}\)
- \(\{103, 104, 105, \ldots\}\)
- ข้อใดเป็นเซตของจำนวนเต็มที่มีค่ามากกว่า 3 และน้อยกว่า 10
- \(\{3, 4, 5, 6, 7, 8, 9, 10\}\)
- \(\{3, 4, 5, 6, 7, 8, 9\}\)
- \(\{4, 5, 6, 7, 8, 9\}\)
- \(\{4, 5, 6, 7, 8, 9, 10\}\)
- เซตของพยัญชนะในคำว่า “เหตุการณ์” คือข้อใด
- \(\{เ, ก, ร, ณ\}\)
- \(\{ก, ร, ณ\}\)
- \(\{ห, ด, ก, ร, ณ\}\)
- \(\{ห, ต, ก, ร, ณ\}\)
- ข้อใดเป็นเซตของจำนวนเต็มที่อยู่ระหว่าง 0 กับ 1
- \(\{0, 1\}\)
- \(\{1\}\)
- \(\{0\}\)
- \(\{\;\}\)
- {มกราคม, มีนาคม, พฤษภาคม, สิงหาคม, ตุลาคม, ธันวาคม} ตรงกับข้อใด
- {x | x เป็นเดือนที่มี 28 วัน}
- {x | x เป็นเดือนที่มี 29 วัน}
- {x | x เป็นเดือนที่มี 30 วัน}
- {x | x เป็นเดือนที่มี 31 วัน}
- {1, 3, 5} ตรงกับข้อใด
- {x | x เป็นจำนวนคี่บวกตั้งแต่ 1 ถึง 5}
- {x | x เป็นจำนวนเต็มตั้งแต่ 1 ถึง 5}
- {x | x เป็นจำนวนนับตั้งแต่ 1 ถึง 5}
- {x | x เป็นจำนวนจริงตั้งแต่ 1 ถึง 5}
- เซตในข้อใดเป็นเซตจำกัด
- {x | x เป็นจำนวนเต็มคู่}
- {x | x เป็นจำนวนเต็มที่หารด้วย 3 ลงตัว}
- {x | x เป็นจำนวนเต็มบวกและน้อยกว่า 1}
- {x | x เป็นจำนวนเต็มคู่ที่น้อยกว่า 1,000}
- เซตในข้อใดเป็นเซตอนันต์
- {x | x เป็นพยัญชนะในภาษาไทย}
- {x | x เป็นจำนวนเต็มที่มากกว่าศูนย์}
- {x | x เป็นเต็มตั้งแต่ 1 ถึง 3}
- {x | x เป็นวันในหนึ่งสัปดาห์}
- เซตของจำนวนเต็มบวกที่น้อยกว่า 0 มีสมาชิกกี่ตัว
- 0
- 1
- 2
- 3
- กำหนด A = {x | x เป็นพยัญชนะในคำว่า “สุดสวย”},
B = {x | x เป็นพยัญชนะในคำว่า “สวยสด”},
C = {x | x เป็นพยัญชนะในคำว่า “สายวาด”},
D = {x | x เป็นพยัญชนะในคำว่า “สายสวย”}
ข้อใดต่อไปนี้เป็นจริง- A = D
- C = D
- B = D
- A = B
- เซตในข้อใดเป็นเซตจำกัด
- {x | x เป็นจำนวนเต็มคู่}
- {x | x เป็นจำนวนเต็มคู่ที่น้อยกว่า 10}
- {x | x เป็นจำนวนเต็มมากกว่า 1}
- {x | x เป็นจำนวนเต็ม และ 3 < x < 10}
- เซตในข้อใดเป็นเซตอนันต์
- {x | x เป็นจำนวนเต็มตั้งแต่ 1 – 3}
- {x | x เป็นจำนวนเต็มลบที่อยู่ระหว่าง -5 กับ 1}
- {x | x เป็นจำนวนเต็มและ 2x = x + 4}
- {x | x เป็นจำนวนเต็มลบ และ x < -1}
- เซตใดต่อไปนี้เป็นเซตว่าง
- เซตของจำนวนเต็มระหว่าง -1 และ 1
- เซตของจำนวนเต็มบวกที่น้อยกว่า 1
- เซตของจำนวนจริงที่ไม่เป็นจำนวนเต็ม
- เซตของจำนวนจริงที่ไม่เป็นจำนวนตรรกยะ
- เซตใดต่อไปนี้ ไม่เป็น เซตว่าง
- {x | x \(\in\) R และ x2 = -1}
- {x | x \(\in\) I และ x + 1 = x}
- {x | x \(\in\) R และ x + x = 0}
- {x | x \(\in\) I และ x2 < 0}
- เซตใดต่อไปนี้ ไม่ถูกต้อง
- เซตว่างเป็นเซตจำกัด
- {0} เป็นเซตว่าง
- {\(\varnothing\), {\(\varnothing\)}, \(\ldots\)} เป็นเซตอนันต์
- {{{ }}} เป็นเซตจำกัด
- เซตใดต่อไปนี้ ไม่ใช่เซตอนันต์
- เซตของจำนวนเต็มลบ
- เซตของจำนวนเฉพาะ
- เซตของจำนวนคู่บวก
- เซตว่าง
- ให้ A = {1, {2}, {1, 2}} ข้อใดผิด
- {2} \(\in\) A
- \(\varnothing \in \varnothing\)
- {{1, 2}} \(\subset\) A
- \(\varnothing \subset\) A
- ให้ B = {1, {3, 5}} ข้อใดเป็นสับเซตของ B
- {1}, {3}, {5}
- {1}, {3, 5}
- { }, {1}, {{3, 5}}, {1, {3, 5}}
- { }, {3, 5}, {1, {3, 5}}
- เซตใดต่อไปนี้เป็นสับเซตของเซต {a, {b}}
- {b}
- {a}
- {{a}, {b}}
- {{a}, {{b}}}
- เซตใดต่อไปนี้ไม่เป็นสับเซตของเซต {\(\varnothing\),1, {1, 2}}
- {{1, 2}}
- {{1}, {1, 2}}
- {\(\varnothing\), {1, 2}}
- {\(\varnothing\), 1, {1, 2}}
- เซตใดต่อไปนี้มีสับเซต 32 เซต
- {\(\varnothing\), {\(\varnothing\)}, 0, {0}, 1}
- {\(\varnothing\), {\(\varnothing\), 0}, {0, 1}}
- {\(\varnothing\), {\(\varnothing\)}, {0, 1}, {1, f}}
- {\(\varnothing\), {1}, {1, 2}, {\(\varnothing\), 1, 2}}
- A = {2, 22, 23, \(\ldots\), 2n} สับเซตแท้ของเซต A มีทั้งหมดกี่สับเซต
- 2n
- 2n-1
- 2n – 1
- n – 1
- กำหนดให้ A = {0, 1} และ B = {1, 2}
ดังนั้น P(A \(\cup\) B) เท่ากับข้อใดต่อไปนี้- {1}
- {\(\varnothing\), 1}
- {\(\varnothing\), {1}}
- {{1}, {2}, {1, 2}}
- กำหนดให้ A = {a} ดังนั้นจานวนสมาชิกของ P(P(P(A)))) เท่ากับข้อใดต่อไปนี้
- 4
- 8
- 16
- 32
- กำหนด A = {1, 2, 3}, B = {2, 3, 4, 5}, C = {1, 2, 5, 6} จงหา A \(\cap\) (B \(\cup\) C)
- {2, 3, 4, 5}
- {1, 2, 5, 6}
- {1, 2, 3}
- {2, 3, 5}
- กำหนดให้ A = {1, 2, 3}, B = {6, 7, 8}
จงหา A \(\cap\) B- { }
- {1, 2, 3}
- {6, 7, 8}
- {1, 2, 3, 6, 7, 8}
- กำหนดให้ \(U\) = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 4, 6, 8} จงหา \((A’)’\)
- { }
- {1, 2, 3, 4, 6, 8}
- {5, 7, 9, 10}
- {1, 2, 3, 4}
- ข้อใดผิด
- เซตว่างเป็นสับเซตของทุกเซต
- เซตที่เป็นสับเซตของเซตว่างต้องเป็นเซตว่าง
- เซตทุกเซตเป็นสับเซตของตัวเอง
- เซตบางเซตเป็นสับเซตของเอกภพสัมพัทธ์
- ให้ \(U\) = {1, 2, 3, 4, 5}, A = {1, 2, 3} และ B = {2, 3, 4} ดังนั้น \((A \cup B)’\) เท่ากับเซตใดต่อไปนี้
- {2}
- {3}
- {5}
- {1, 2, 3, 4}
- ให้ \(U\) = {a, e, i, o, u}, A = {a, e, i} และ B = {e, i, o} ดังนั้น \((A \cap B)’\) เท่ากับเซตใดต่อไปนี้
- {a, e}
- {e, i}
- {i, o, u}
- {a, o, u}
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
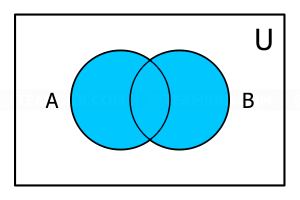
- \(A \cup B\)
- \(A \cap B\)
- \(A \; – B\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
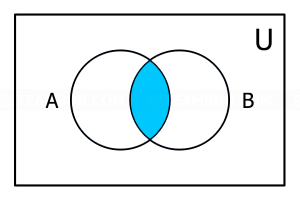
- \(A \cup B\)
- \(A \cap B\)
- \(A \; – B\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
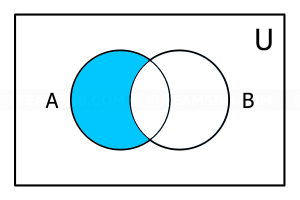
- \(A \cup B\)
- \(A \cap B\)
- \(A \; – B\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
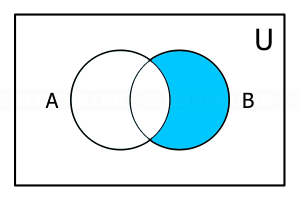
- \(A \cup B\)
- \(A \cap B\)
- \(A \; – B\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
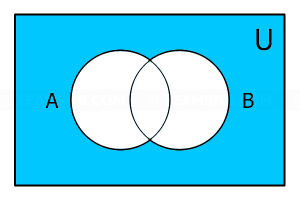
- \((A \cup B)’\)
- \((A \cap B)’\)
- \(A \; – B\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
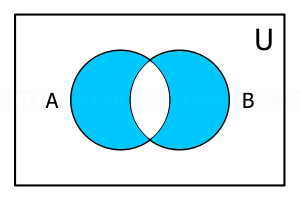
- \((A \cup B)’\)
- \((A \; – B) \cup (B \; – A)\)
- \((A \cap B)’\)
- \(B \; – A\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
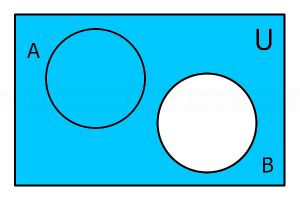
- \((A \cup B)’\)
- \(A \; – B\)
- \((A \cap B)’\)
- \(B’\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
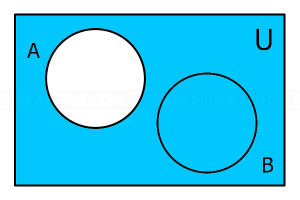
- \((A \cup B)’\)
- \(A \; – B\)
- \((A \cap B)’\)
- \(A’\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
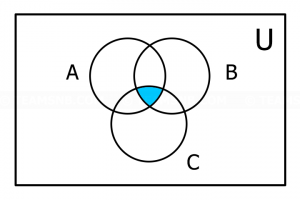
- \(A \cup B \cup C\)
- \(A \cap B \cap C\)
- \((A \cap B) \cup C\)
- \((A \cup B) \cap C\)
- จากแผนภาพนี้ ส่วนที่แรเงาตรงกับข้อใด
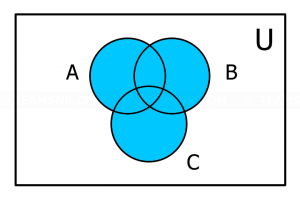
- \(A \cup B \cup C\)
- \(A \cap B \cap C\)
- \((A \cap B) \cup C\)
- \((A \cup B) \cap C\)
ใช้ข้อมูลต่อไปนี้ ตอบคำถามข้อ 41-44
จากการสอบถามนักเรียน 205 คน พบว่าเรียนฟิสิกส์ 52 คน
เรียนเคมี 30 คน
เรียนคณิตศาสตร์และเคมี 26 คน
เรียนคณิตศาสตร์และฟิสิกส์ 45 คน
เรียนคณิตศาสตร์, ฟิสิกส์ และเคมี 5 คน
และ 96 คนไม่ได้เรียนวิชาใดในสามวิชานี้เลย
และ ไม่มีผู้ใดเรียนฟิสิกส์และเคมี แล้วไม่เรียนคณิตศาสตร์
- มีนักเรียนกี่คนที่เรียนเคมีอย่างเดียว
- 2 คน
- 4 คน
- 5 คน
- 8 คน
- มีนักเรียนกี่คนที่เรียนหนึ่งรายวิชาในสามรายวิชาข้างต้น
- 40 คน
- 41 คน
- 42 คน
- 43 คน
- มีนักเรียนกี่คนที่เรียนสองรายวิชาในสามรายวิชาข้างต้น
- 40 คน
- 43 คน
- 61 คน
- 65 คน
- มีนักเรียนกี่คนที่เรียนคณิตศาสตร์วิชาเดียว
- 16 คน
- 26 คน
- 30 คน
- 32 คน
ใช้ข้อมูลต่อไปนี้ ตอบคำถามข้อ 45-47
นักเรียนห้องหนึ่งมี 30 คน เรียนคณิตศาสตร์ 19 คน
เรียนเคมี 17 คน
เรียนชีววิทยา 11 คน
เรียนคณิตศาสตร์และเคมี 12 คน
เรียนชีววิทยาและคณิตศาสตร์ 7 คน
เรียนเคมีและชีววิทยา 5 คน
และ 2 คนเรียนทั้งสามวิชา
- มีนักเรียนกี่คนที่เรียนคณิตศาสตร์ แต่ไม่เรียนวิชาเคมี
- 7 คน
- 8 คน
- 9 คน
- 10 คน
- มีนักเรียนกี่คนเรียนสองรายวิชา
- 16 คน
- 18 คน
- 19 คน
- 20 คน
- มีนักเรียนกี่คนที่เรียนวิชาเดียวหรือไม่เรียนเลย
- 7 คน
- 8 คน
- 10 คน
- 11 คน
- มีนักเรียนกี่คนที่เรียนคณิตศาสตร์วิชาเดียว
- 16 คน
- 26 คน
- 30 คน
- 32 คน
- มีนักเรียน 40 คน สอบวิชาฟิสิกส์ไม่ผ่าน 10 คน สอบวิชาคณิตศาสตร์ไม่ผ่าน 7 คน และสอบไม่ผ่านทั้งสองวิชา 4 คน มีนักเรียนกี่คนที่สอบผ่านทั้งสองวิชา
- 25 คน
- 26 คน
- 27 คน
- 29 คน