ในการหาพื้นที่ระหว่างเส้นโค้ง เราจะเป็นแบ่งเป็น 2 กรณี คือ
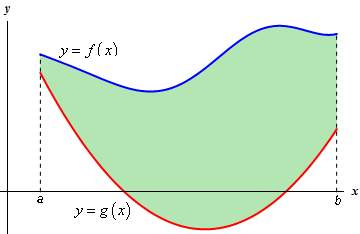
- กำหนดให้ \(y_1 = f(x)\) และ \(y_2 = g(x)\) เป็นฟังก์ชันต่อเนื่อง โดยที่ \(f(x) \geq g(x)\) สำหรับทุกค่า \(x \in [a,b]\) เราจะหาพื้นที่ซึ่งถูกปิดล้อมด้วยเส้นโค้ง \(f(x)\) และ \(g(x)\) ได้จากสูตร
\(A = \int_a^b \Bigl[f(x) \; – g(x)\Bigl] \; dx\)
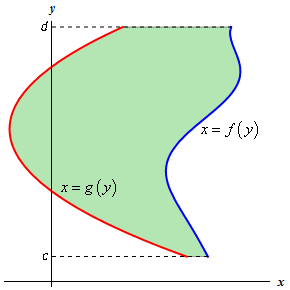
- กำหนดให้ \(x_1 = f(y)\) และ \(x_2 = g(y)\) เป็นฟังก์ชันต่อเนื่อง โดยที่ \(f(y) \geq g(y)\) สำหรับทุกค่า \(y \in [c,d]\) เราจะหาพื้นที่ซึ่งถูกปิดล้อมด้วยเส้นโค้ง \(f(y)\) และ \(g(y)\) ได้จากสูตร
\(A = \int_c^d \Bigl[f(y) \; – g(y)\Bigl] \; dy\)
ถ้าเราวาดรูปกราฟไม่ได้ เราสามารถคำนวนว่าสมการใดมีค่ามากกว่าได้ดังนี้
- หาจุดตัดระหว่างกราฟทั้ง 2 โดยจับสมการเท่ากัน แล้วแก้สมการหาค่า x (หรือ y)
- นำค่าตัวเลขหนึ่งตัวที่อยู่ระหว่างค่า x (หรือ y) ที่คำนวนได้ในข้อ 1 แทนลงสมการทั้งสอง ถ้าสมการใดมีค่ามากกว่า แสดงว่าสมการนั้นอยู่ด้านบน
ตัวอย่าง จงหาพื้นที่ที่อยู่ระหว่างกราฟ \(y=x\) และ \(y=x^2\)
ดูคำตอบ
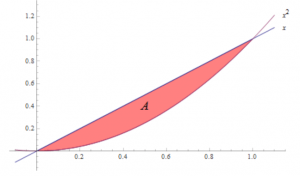
วิธีทำ
- หาจุดตัดระหว่างกราฟทั้ง 2
\(\quad \begin{align*}x & = x^2 \\
x^2 \;- x &= 0 \\
x(x \; -1) &= 0 \\
x &= 0, 1
\end{align*}\)
- เลือก \(x = \frac{1}{2},\)
\(
\begin{align*}
\qquad y &= x = \frac{1}{2} \\
y &= x^2 = \Bigl(\frac{1}{2}\Bigl)^2 = \frac{1}{4}
\end{align*}
\)
เราจะได้ว่าสมการ \(y=x\) มากกว่าสมการ \(y=x^2\) ในช่วง \(x \in [0,1]\)
- คำนวนหาพื้นที่ได้จากสูตร
\(\begin{align*}
\quad A &= \int_a^b \Bigl[f(x) \; – g(x)\Bigl] \; dx \\[6pt]
&= \int_0^1 \Bigl[x \; – x^2\Bigl] \; dx \\[6pt]
&= \biggl[\frac{x^2}{2} \; – \frac{x^3}{3}\biggl]_0^1 \\[6pt]
&= \frac{1}{2} \; – \frac{1}{3} \\[6pt]
&= \frac{1}{6}
\end{align*}
\)
จงหาพื้นที่ที่ถูกปิดล้อมด้วย \(y=x \; -x^2\) และ \(x + y = 0\)
ดูคำตอบ
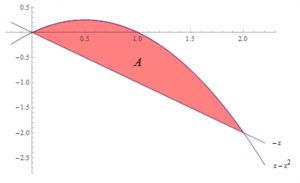
วิธีทำ
- หาจุดตัดระหว่างกราฟทั้ง 2
\(\quad \begin{align*}x \; – x^2 & = -x \\
x^2 \; – 2x &= 0 \\
x(x \; – 2) &= 0 \\
x &= 0, 2
\end{align*}\)
- เลือก \(x = 1,\)
\(
\begin{align*}
\qquad y &= x \; – x^2 = 1 \; – 1^2 = 0 \\
y &= -x = -1
\end{align*}
\)
เราจะได้ว่าสมการ \(y=x \; – x^2\) มากกว่าสมการ \(x + y = 0\) ในช่วง \(x \in [0,2]\)
- คำนวนหาพื้นที่ได้จากสูตร
\(\begin{align*}
\quad A &= \int_a^b \Bigl[f(x) \; – g(x)\Bigl] \; dx \\[6pt]
&= \int_0^2 \Bigl[x \; – x^2 \; – (-x)\Bigl] \; dx \\[6pt]
&= \int_0^2 \Bigl[2x \; – x^2 \Bigl] \; dx \\[6pt]
&= \biggl[\frac{2x^2}{2} \; – \frac{x^3}{3}\biggl]_0^2 \\[6pt]
&= 4 \; – \frac{8}{3} \\[6pt]
&= \frac{4}{3}
\end{align*}
\)
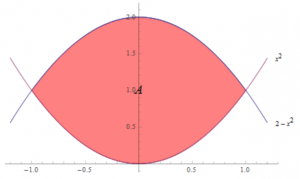
จงหาพื้นที่ที่ถูกปิดล้อมด้วย \(y = 2 \; – x^2\) และ \(y = x^2\)
ดูคำตอบ
วิธีทำ
- หาจุดตัดระหว่างกราฟทั้ง 2
\(\quad \begin{align*}2 \; – x^2 & = x^2 \\
2x^2 \; – 2 &= 0 \\
2(x^2 \; – 1) &= 0 \\
x &= 1, -1
\end{align*}\)
- เลือก \(x = 0,\)
\(
\begin{align*}
\qquad y &= 2 \; – (0)^2 = 2 \\
y &= (0)^2 = 0
\end{align*}
\)
เราจะได้ว่าสมการ \(y = 2 \; – x^2\) มากกว่าสมการ \(y = x^2\) ในช่วง \(x \in [-1,1]\)
- คำนวนหาพื้นที่ได้จากสูตร
\(\begin{align*}
\quad A &= \int_a^b \Bigl[f(x) \; – g(x)\Bigl] \; dx \\[6pt]
&= \int_{-1}^1 \Bigl[2 \; – x^2 \; – (x^2)\Bigl] \; dx \\[6pt]
&= \int_{-1}^1 \Bigl[2 \; – 2x^2 \Bigl] \; dx \\[6pt]
&= \biggl[2x \; – \frac{2x^3}{3}\biggl]_{-1}^1 \\[6pt]
&= \Bigl(2 \; – \frac{2}{3}\Bigl) \; – \Bigl(-2 \; – \frac{2(-1)}{3}\Bigl) \\[6pt]
&= \frac{4}{3} \; – \Bigl(-2 + \frac{2}{3}\Bigl)\\[6pt]
&= \frac{8}{3}
\end{align*}
\)
จงหาพื้นที่ที่ถูกปิดล้อมด้วย \(y = \sin x\) และ \(y = \cos x\) บนช่วง \(x \in \Bigl[0,\frac{\pi}{2}\Bigl]\)
ดูคำตอบ
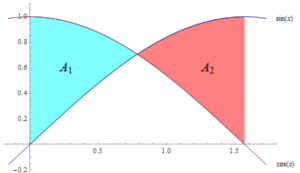
ในกรณี \(f(x) \geq g(x)\) สำหรับบางค่าของค่า \(x\) และ \(g(x) \geq f(x)\) สำหรับบางค่าของค่า \(x\) เราต้องแยกคำนวนพื้นที่ออกเป็นช่วงๆ \(A_1, A_2, \ldots\) แล้วค่อยนำผลลัพธ์ที่ได้มารวมกันเป็นพื้นที่ที่ถูกปิดล้อมทั้งหมด \(A = A_1 + A_2 + \ldots\)
วิธีทำ
- หาจุดตัดระหว่างกราฟทั้ง 2
\(\quad \begin{align*} \sin x & = \cos x \\[6pt]
\frac{\sin x}{\cos x} &= 1 \\[6pt]
\tan x &= 1 \\[6pt]
x &= \frac{\pi}{4}
\end{align*}\)
- พิจารณาพื้นที่ \(A_1\) โดยเลือก \(x = \frac{\pi}{6},\)
\(
\begin{align*}
\qquad y &= \sin \frac{\pi}{6} = \frac{1}{2} = 0.5 \\
y &= \cos \frac{\pi}{6} = \frac{\sqrt{3}}{2} \approx 0.866
\end{align*}
\)
เราจะได้ว่าสมการ \(y = \cos x\) มากกว่าสมการ \(y = \sin x\) ในช่วง \(x \in [0,\frac{\pi}{4}]\)
- พิจารณาพื้นที่ \(A_2\) โดยเลือก \(x = \frac{\pi}{3},\)
\(
\begin{align*}
\qquad y &= \sin \frac{\pi}{3} = \frac{\sqrt{3}}{2} \approx 0.866 \\
y &= \cos \frac{\pi}{3} = \frac{1}{2} = 0.5
\end{align*}
\)
เราจะได้ว่าสมการ \(y = \sin x\) มากกว่าสมการ \(y = \cos x\) ในช่วง \(x \in [\frac{\pi}{4},\frac{\pi}{2}]\)
- คำนวนหาพื้นที่ได้จากสูตร
\(\begin{align*}
\quad A &= A_1 + A_2 \\[6pt]
&= \int_{0}^{\frac{\pi}{4}} \Bigl(\cos x \; – \sin x\Bigl) \; dx + \int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \Bigl(\sin x \; – \cos x\Bigl) \; dx\\[6pt]
&= \biggl[\sin x + \cos x\biggl]_{0}^{\frac{\pi}{4}} + \biggl[- \cos x \; – \sin x\biggl]_{\frac{\pi}{4}}^{\frac{\pi}{2}} \\[6pt]
&= \biggl[\Bigl(\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\Bigl) \; – 1\biggl] \; – \biggl[\Bigl(0 + 1\Bigl) \; – \Bigl(\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\Bigl)\biggl] \\[6pt]
&= 2\sqrt{2} \; – 2
\end{align*}
\)
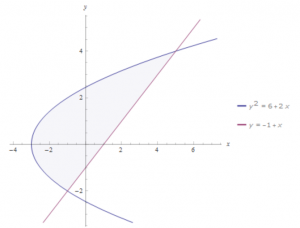
จงหาพื้นที่ที่ถูกปิดล้อมด้วย \(y = x \; – 1\) และ \(y^2 = 2x + 6\)
ดูคำตอบ
วิธีทำ
- หาจุดตัดระหว่างกราฟทั้ง 2
\(\quad \begin{align*}y + 1 & = \frac{y^2 \; – 6}{2} \\[6pt]
2y + 2 &= y^2 \; – 6 \\[6pt]
y^2 \; – 2y \; – 8 &= 0 \\[6pt]
(y \; – 4)(y + 2) &= 0 \\[6pt]
y &= 4, -2
\end{align*}\)
- เลือก \(y = 0,\)
\(
\begin{align*}
\qquad x &= 0 + 1 = 1 \\
x &= \frac{(0)^2 \; – 6}{2} = -3
\end{align*}
\)
เราจะได้ว่าสมการ \(y = x \; – 1\) มากกว่าสมการ \(y^2 = 2x + 6\) ในช่วง \(y \in [-2,4]\)
- คำนวนหาพื้นที่ได้จากสูตร
\(\begin{align*}
\quad A &= \int_c^d \Bigl[f(y) \; – g(y)\Bigl] \; dy \\[6pt]
&= \int_{-2}^4 \Bigl[(y + 1) \; – \Bigl(\frac{y^2 \; – 6}{2}\Bigl)\Bigl] \; dy \\[6pt]
&= \int_{-2}^4 \Bigl[y + 1 \; – \frac{y^2}{2} + 3\Bigl] \; dy \\[6pt]
&= \int_{-2}^4 \Bigl[y \; – \frac{y^2}{2} + 4\Bigl] \; dy \\[6pt]
&= \biggl[\frac{y^2}{2} \; – \frac{y^3}{6} + 4y\biggl]_{-2}^4 \\[6pt]
&= \Bigl(\frac{16}{2} \; – \frac{64}{6} +16\Bigl) \; – \Bigl(\frac{4}{2} + \frac{8}{6} \; – 8\Bigl)\\[6pt]
&= 6 \; – \frac{72}{6} + 24 \\[6pt]
&= 18
\end{align*}
\)






