1. ประพจน์
ประพจน์ คือ ประโยคที่เป็นจริงหรือเท็จอย่างใดอย่างหนึ่งเท่านั้น และประโยคเหล่านี้อาจจะอยู่ในรูปประโยคบอกเล่าหรือประโยคปฏิเสธก็ได้ เช่น
- แมวมี 4 ขา → เป็นประพจน์ เพราะบอกได้ว่าเป็นจริง
- 3 + 6 = 9 → เป็นประพจน์ เพราะบอกได้ว่าเป็นจริง
- 15 เป็นจำนวนเต็ม → เป็นประพจน์ เพราะบอกได้ว่าเป็นจริง
- เชียงรายเป็นประเทศ → เป็นประพจน์ เพราะบอกได้ว่าเป็นเท็จ
- 12 – 8 = 20 → เป็นประพจน์ เพราะบอกได้ว่าเป็นเท็จ
ประโยคที่ไม่ใช่ประพจน์ คือ ประโยคที่ไม่สามารถบอกได้ว่าเป็นจริงหรือเท็จ เช่น ประโยคคำถาม คำสั่ง คำขอร้อง คำอุทาน สุภาษิต รวมถึงประโยคที่มีตัวแปร ซึ่งไม่สามารถบอกว่าเป็นจริงหรือเท็จ เรียกว่าประโยคเปิด เช่น
- คุณมีเงินในกระเป๋าเท่าไหร่ → ไม่เป็นประพจน์ เพราะเป็นประโยคคำถาม
- พรุ่งนี้ครูให้ทำรายงาน → ไม่เป็นประพจน์ เพราะเป็นประโยคคำสั่ง
- กรุณาปิดประตูเบาๆ → ไม่เป็นประพจน์ เพราะเป็นคำขอร้อง
- พระเจ้าช่วย → ไม่เป็นประพจน์ เพราะเป็นคำอุทาน
- ไก่เห็นตีนงู งูเห็นนมไก่ → ไม่เป็นประพจน์ เพราะเป็นสุภาษิต
- 20 – x = 5 → ไม่เป็นประพจน์ เพราะเป็นมีตัวแปร (ถ้า x เป็น 15 จะเป็นจริง แต่ถ้า x เป็น 10 จะเป็นเท็จ)
- เขาเป็นนักกีฬา → ไม่เป็นประพจน์ เพราะเป็นประโยคเปิด (ไม่รู้ว่าเขาเป็นใคร ดังนั้น เราไม่สามารถบอกได้ว่าจริงหรือเท็จ)
จงพิจารณาว่า ข้อใดต่อไปนี้เป็นประพจน์
- เลข 1 เป็นจำนวนเฉพาะ
- ปิดหน้าต่างให้หน่อย
- ช่วยกันรักษาความสะอาด
- โปรดเมตตาด้วยเถิด
- เชียงรายเป็นประเทศ
- หนึ่งวัน มี 30 ชั่วโมง
- 1/2 มีค่าเท่ากับ 0.5
- เขาเป็นคนดี
- 0.75 เป็นเศษส่วน
- 2x – 4y = 20
- จงยืนขึ้น
- ดาวอังคารเป็นดาวเคราะห์
2. การเชื่อมประพจน์
กำหนดให้ \(P\) และ \(Q\) เป็นประพจน์ เมื่อนำทั้ง 2 ประพจน์มาเชื่อมกันด้วยตัวเชื่อมแล้ว เราจะได้ประพจน์เชิงประกอบ ซึ่งสามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ โดยตัวเชื่อมที่ใช้มี 5 ตัว คือ
- ตัวเชื่อมประพจน์ “และ” (Conjunction) ใช้สัญลักษณ์ \(\land\)
\(P \land Q\) จะมีค่าความจริงเป็นจริง เมื่อ \(P\) และ \(Q\) มีค่าความจริงเป็นจริงเท่านั้น นอกนั้นมีค่าความจริงเป็นเท็จ - ตัวเชื่อมประพจน์ “หรือ” (Disjunction) ใช้สัญลักษณ์ \(\lor\)
\(P \lor Q\) จะมีค่าความจริงเป็นเท็จ เมื่อ \(P\) และ \(Q\) มีค่าความจริงเป็นเท็จเท่านั้น นอกนั้นมีค่าความจริงเป็นจริง - ตัวเชื่อมประพจน์ “ถ้า…แล้ว” (Conditional) ใช้สัญลักษณ์ \(\to\)
\(P \to Q\) จะมีค่าความจริงเป็นเท็จ เมื่อ \(P\) เป็นจริง และ \(Q\) เป็นเท็จ นอกนั้นมีค่าความจริงเป็นจริง - ตัวเชื่อมประพจน์ “ก็ต่อเมื่อ” (Biconditional) ใช้สัญลักษณ์ \(\leftrightarrow\)
\(P \leftrightarrow Q\) จะมีค่าความจริงเป็นจริง เมื่อ \(P\) และ \(Q\) มีค่าความจริงตรงกัน และจะมีค่าความจริงเป็นเท็จ เมื่อ \(P\) และ \(Q\) มีค่าความจริงตรงข้ามกัน - นิเสธของประพจน์ “ไม่” (Negation) ใช้สัญลักษณ์ \(\sim\)
ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์นั้นๆ เขียนอยู่ในรูป \({\sim}P\) เช่น
ถ้า \(P\) มีค่าความจริงเป็นจริง \({\sim}P\) จะมีค่าความจริงเป็นเท็จ
ถ้า \(P\) มีค่าความจริงเป็นเท็จ \({\sim}P\) จะมีค่าความจริงเป็นจริง
3. ตารางค่าความจริง
ตารางที่บอกค่าความในทุกๆกรณีของประพจน์ที่เราสนใจ| \(P\) | \(Q\) | \(P \land Q\) | \(P \lor Q\) | \(P \to Q\) | \(P \leftrightarrow Q\) |
|---|---|---|---|---|---|
| \(T\) | \(T\) | \(\underline{T}\) | \(T\) | \(T\) | \(\underline{T}\) |
| \(T\) | \(F\) | \(F\) | \(T\) | \(\underline{F}\) | \(F\) |
| \(F\) | \(T\) | \(F\) | \(T\) | \(T\) | \(F\) |
| \(F\) | \(F\) | \(F\) | \(\underline{F}\) | \(T\) | \(\underline{T}\) |
4. สมมูล
สมมูล เขียนแทนด้วยสัญลักษณ์ \(\equiv\) แปลว่า “มีค่าความจริงเหมือนกัน”
ประพจน์สองประพจน์ใด จะสมมูลกันก็ต่อเมื่อประพจน์ทั้งสองมีค่าความจริงเหมือนกันทุกกรณี การตรวจสอบว่าประพจน์สมมูลกันหรือไม่ ทำได้ 2 วิธี คือ
- ใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ต่อไปนี้สมมูลกันหรือไม่
- \({\sim}P \to Q\) กับ \( {\sim}Q \to P\)
\(\therefore\) จากตาราง จะเห็นได้ว่าประพจน์ \({\sim}P \to Q\) สมมูลกับประพจน์ \( {\sim}Q \to P\) เพราะมีค่าความจริงเหมือนกันทุกกรณี เขียนแทนด้วยสัญลักษณ์ \({\sim}P \to Q \equiv {\sim}Q \to P \)
\(P\) \(Q\) \({\sim}P\) \({\sim}Q\) \({\sim}P \to Q\) \({\sim}Q \to P\) \(T\) \(T\) \(F\) \(F\) \(\color{blue}{T}\) \(\color{blue}{T}\) \(T\) \(F\) \(F\) \(T\) \(\color{blue}{T}\) \(\color{blue}{T}\) \(F\) \(T\) \(T\) \(F\) \(\color{blue}{T}\) \(\color{blue}{T}\) \(F\) \(F\) \(T\) \(T\) \(\color{blue}{F}\) \(\color{blue}{F}\) - \(P \to Q\) กับ \( {\sim}P \land Q\)
\(\therefore\) จากตาราง จะเห็นได้ว่าประพจน์ \(P \to Q\) ไม่สมมูลกับประพจน์ \( {\sim}P \land Q\) เพราะมีค่าความจริงในบางกรณีต่างกัน
\(P\) \(Q\) \({\sim}P\) \(P \to Q\) \({\sim}P \land Q\) \(T\) \(T\) \(F\) \(\color{blue}{T}\) \(\color{blue}{F}\) \(T\) \(F\) \(F\) \(\color{blue}{F}\) \(\color{blue}{F}\) \(F\) \(T\) \(T\) \(\color{blue}{T}\) \(\color{blue}{T}\) \(F\) \(F\) \(T\) \(\color{blue}{T}\) \(\color{blue}{F}\)
ข้อควรรู้ถ้าประพจน์สองประพจน์มีตารางค่าความจริงเหมือนกันทุกกรณี เราจะสรุปได้ว่าทั้งสองประพจน์นั้นสมมูลกัน
ถ้าประพจน์สองประพจน์มีตารางค่าความจริงตรงกันข้ามกันทุกกรณี เราจะสรุปได้ว่าทั้งสองประพจน์นั้นเป็นคู่นิเสธกัน - \({\sim}P \to Q\) กับ \( {\sim}Q \to P\)
- ใช้รูปแบบของประพจน์ที่สมมูลกัน โดยรูปแบบของประพจน์ที่สมมูลกันที่สำคัญ เช่น
- \(P \land Q \equiv Q \land P\)
- \(P \lor Q \equiv Q \lor P\)
- \((P \land Q) \land R \equiv P \land (Q \land R)\)
- \((P \lor Q) \lor R \equiv P \lor (Q \lor R)\)
- \(P \land (Q \lor R) \equiv (P \land Q) \lor (P \land R)\)
- \(P \lor (Q \land R) \equiv (P \lor Q) \land (P \lor R)\)
- \(P \to Q \equiv {\sim}P \lor Q\)
- \(P \to Q \equiv {\sim}Q \to {\sim}P\)
- \(P \leftrightarrow Q \equiv (P \to Q) \land (Q \to P)\)
- \(P \lor Q\) กับ \( {\sim}Q \to P\)
วิธีทำ
- จาก \( \quad P \to Q \equiv {\sim}P \lor Q\)
- \(\begin{align*}
\quad {\sim}Q \to P &\equiv {\sim}({\sim}Q) \lor P \\
&\equiv Q \lor P \\
&\equiv P \lor Q \\
\end{align*}
\) - ดังนั้น ประพจน์ทั้งคู่สมมูลกัน
- \(P \leftrightarrow Q\) กับ \(({\sim}P \lor Q) \land (P \lor {\sim}Q)\)
วิธีทำ
- จาก \( \quad P \leftrightarrow Q \equiv (P \to Q) \land (Q \to P)\;\) และ \(\;P \to Q \equiv {\sim}P \lor Q\)
- \(\begin{align*}
\quad P \leftrightarrow Q &\equiv (P \to Q) \land (Q \to P) \\
&\equiv ({\sim}P \lor Q) \land ({\sim}Q \lor P)\\
&\equiv ({\sim}P \lor Q) \land (P \lor {\sim}Q)\\
\end{align*}
\) - ดังนั้น ประพจน์ทั้งคู่สมมูลกัน
- \(P \to (Q \to R)\) กับ \((P \land Q) \to R\)
วิธีทำ
- \(\begin{align*}
\quad P \to (Q \to R) &\equiv {\sim}P \lor (Q \to R) \\
&\equiv {\sim}P \lor ({\sim}Q \lor R) \\
&\equiv {\sim}P \lor {\sim}Q \lor R \\ \\
\quad (P \land Q) \to R &\equiv {\sim}(P \land Q) \lor R \\
&\equiv ({\sim}P \lor {\sim}Q) \lor R \\
&\equiv {\sim}P \lor {\sim}Q \lor R
\end{align*}
\) - ดังนั้น ประพจน์ทั้งคู่สมมูลกัน
- \(\begin{align*}
- \({\sim}P \land (Q \lor P)\) กับ \({\sim}(Q \to P)\)
วิธีทำ
- \(\begin{align*}
\quad {\sim}P \land (Q \lor P) &\equiv ({\sim}P \land Q) \lor ({\sim}P \land P) \\
&\equiv ({\sim}P \land Q) \lor F \\
&\equiv {\sim}P \land Q \\ \\
\quad {\sim}(Q \to P) &\equiv {\sim}({\sim}Q \lor P)) \\
&\equiv Q \land {\sim}P \\
&\equiv {\sim}P \land Q
\end{align*}
\) - ดังนั้น ประพจน์ทั้งคู่สมมูลกัน
- \(\begin{align*}
- \(P \to (Q \to R)\) กับ \((P \to Q) \to R\)
วิธีทำ
- \(\begin{align*}
\quad P \to (Q \to R) &\equiv {\sim}P \lor (Q \to R) \\
&\equiv {\sim}P \lor ({\sim}Q \lor R) \\
&\equiv {\sim}P \lor {\sim}Q \lor R
\end{align*}
\)ประพจน์นี้จะเป็นเท็จ เมื่อ \(P\) เป็นจริง \(Q\) เป็นจริง และ \(R\) เป็นเท็จเท่านั้น
\(\begin{align*}
\quad (P \to Q) \to R &\equiv ({\sim}P \lor Q) \to R) \\
&\equiv {\sim}({\sim}P \lor Q) \lor R) \\
&\equiv (P \land {\sim}Q) \lor R
\end{align*}
\)ประพจน์นี้เป็นเท็จได้หลายกรณี เช่น \(P\) เป็นเท็จ \(Q\) เป็นเท็จ และ \(R\) เป็นเท็จ
- ดังนั้น ประพจน์ทั้งคู่ไม่สมมูลกัน
- \(\begin{align*}
4. สัจนิรันดร์ (Tautology)
ประพจน์ที่เป็นสัจนิรันดร์ หมายถึง ประพจน์ที่มีค่าความจริงเป็นจริงทุกกรณี
การตรวจสอบสัจนิรันดร์ทำได้ 2 วิธี
- การตรวจสอบโดยใช้ตารางแสดงค่าความจริง
ตัวอย่าง จงตรวจสอบว่าประพจน์ \((P \to Q) \leftrightarrow ({\sim}Q \to {\sim}P)\) เป็นสัจนิรันดร์หรือไม่
\(P\) \(Q\) \(P \to Q\) \({\sim}Q\) \({\sim}P\) \({\sim}Q \to {\sim}P\) \((P \to Q) \leftrightarrow ({\sim}Q \to {\sim}P)\) \(T\) \(T\) \(T\) \(F\) \(F\) \(T\) \(\color{blue}{T}\) \(T\) \(F\) \(F\) \(T\) \(F\) \(F\) \(\color{blue}{T}\) \(F\) \(T\) \(T\) \(F\) \(T\) \(T\) \(\color{blue}{T}\) \(F\) \(F\) \(T\) \(T\) \(T\) \(T\) \(\color{blue}{T}\) จากตาราง จะเห็นได้ว่าทุกกรณีที่เป็นไปได้ มีค่าความจริงเป็นจริงทั้งหมด
\(\therefore\) ประพจน์ \((P \to Q) \leftrightarrow ({\sim}Q \to {\sim}P)\) เป็นสัจนิรันดร์ - การตรวจสอบโดยวิธีหาข้อขัดแย้ง
สมมติให้ประพจน์ที่ต้องการตรวจสอบสัจนิรันดร์ เป็นเท็จ และหาค่าความจริงของประพจน์ย่อย
ถ้าค่าความจริงของประพจน์ย่อยขัดแย้งกันในทุกกรณี จะสรุปว่าเป็นสัจนิรันดร์
แต่ถ้าค่าความจริงของประพจน์ย่อยไม่ขัดแย้งกัน (อย่างน้อย 1 กรณี) หรือหาค่าความจริงของประพจน์ย่อยไม่ได้ จะสรุปว่าไม่เป็นสัจนิรันดร์ ตัวอย่าง จงตรวจสอบว่าประพจน์ \(P \to (P \lor Q)\) เป็นสัจนิรันดร์หรือไม่วิธีทำตัวอย่าง จงตรวจสอบว่าประพจน์ \((P \land Q) \leftrightarrow (P \lor Q)\) เป็นสัจนิรันดร์หรือไม่- สมมติให้ประพจน์มีค่าความจริงเป็นเท็จ
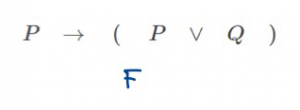
- จากตัวเชื่อมประพจน์ \(\to\) เราจะได้ว่าประพจน์ด้านหน้า \((P)\) ต้องมีค่าเป็นจริง และ ประพจน์ด้านหลัง \((P \lor Q)\) ต้องมีค่าเป็นเท็จเท่านั้น
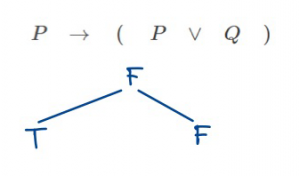
- เมื่อพิจารณาประพจน์ด้านหลัง \((P \lor Q)\) จะมีค่าความจริงเป็นเท็จ ก็ต่อเมื่อ \(P\) และ \(Q\) เป็นเท็จ แต่จากประพจน์ด้านหน้า \(P\) มีค่าความจริงเป็นจริง ทำให้ค่าความจริงของประพจน์ \(P\) ขัดแย้งกัน
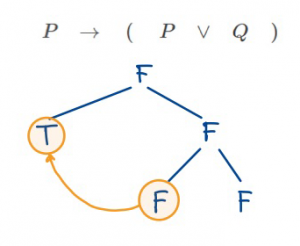
\(\therefore\) เราจึงสรุปได้ว่าประพจน์นี้เป็นสัจนิรันดร์
วิธีทำ- สมมติให้ประพจน์มีค่าความจริงเป็นเท็จ
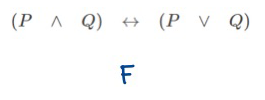
- จากตัวเชื่อมประพจน์ \(\leftrightarrow\) จะเป็นเท็จได้สองกรณี คือ ประพจน์ด้านหน้าเป็นจริงและประพจน์ด้านหลังเป็นเท็จ หรือ ประพจน์ด้านหน้าเป็นเท็จและประพจน์ด้านหลังเป็นจริง
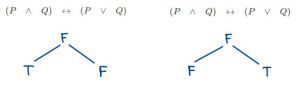
- เมื่อพิจารณากรณีแรก เราพบข้อขัดแย้ง ทำให้เรายังไม่สามารถสรุปว่าข้อนี้เป็นสัจนิรันดร์หรือไม่ เพราะเราต้องไปพิจารณากรณีที่สองด้วย
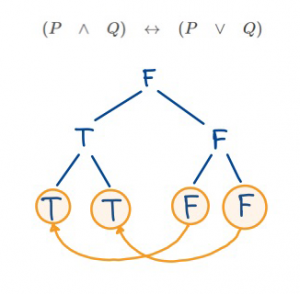
- เมื่อพิจารณากรณีที่สอง เราสามารถแบ่งได้เป็น 2 กรณีย่อยคือ
- \(P\) มีค่าความจริงเป็นเท็จ และ \(Q\) มีค่าความจริงเป็นจริง
- \(P\) มีค่าความจริงเป็นจริง และ \(Q\) มีค่าความจริงเป็นเท็จ
ทั้ง 2 กรณีย่อยไม่เกิดข้อแย้ง แสดงว่าประพจน์ที่โจทย์กำหนดสามารถมีค่าความจริงเป็นเท็จได้
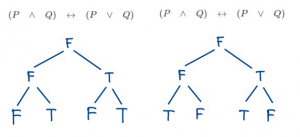
\(\therefore\) เราจึงสรุปได้ว่าประพจน์นี้เป็นไม่เป็นสัจนิรันดร์
- สมมติให้ประพจน์มีค่าความจริงเป็นเท็จ