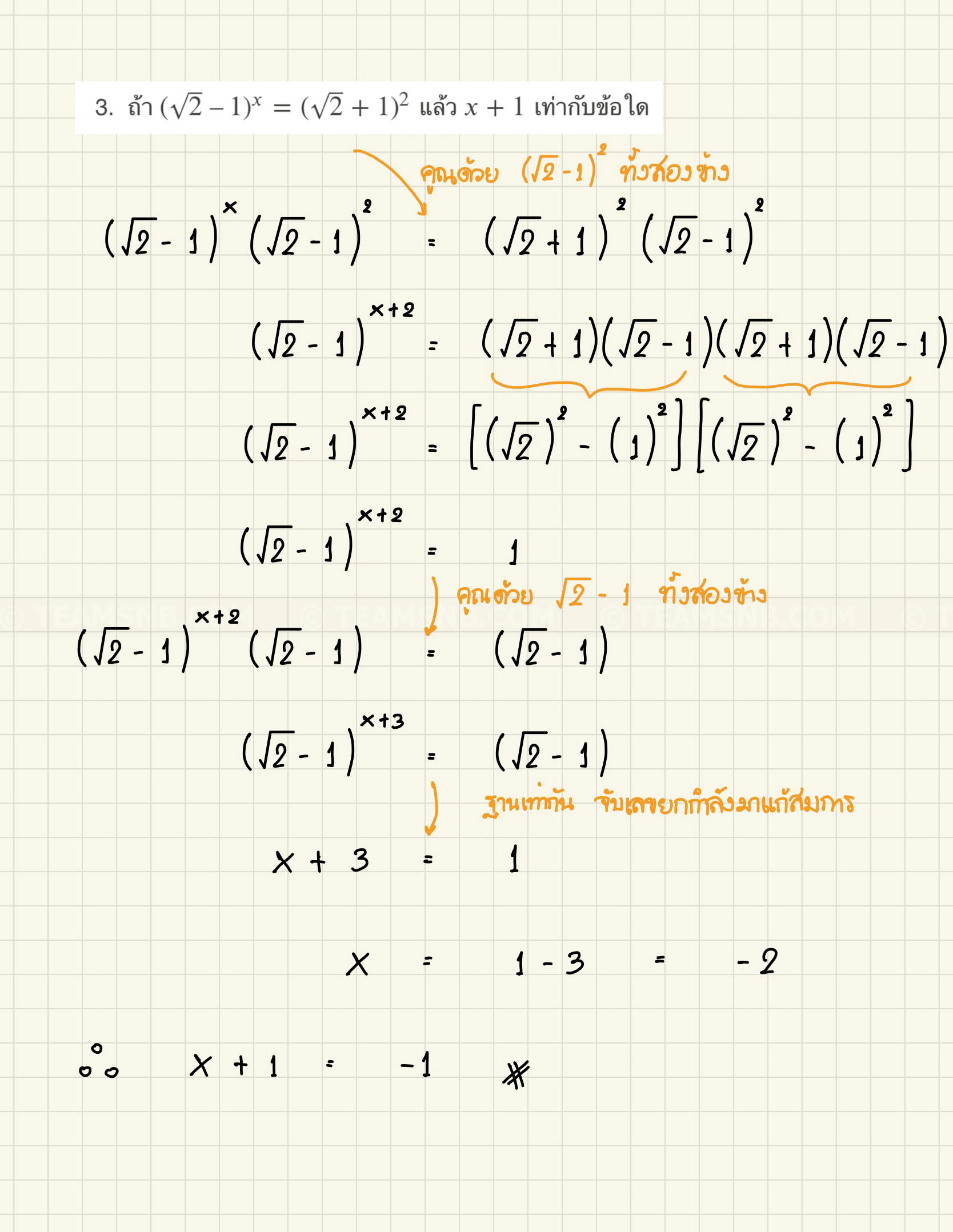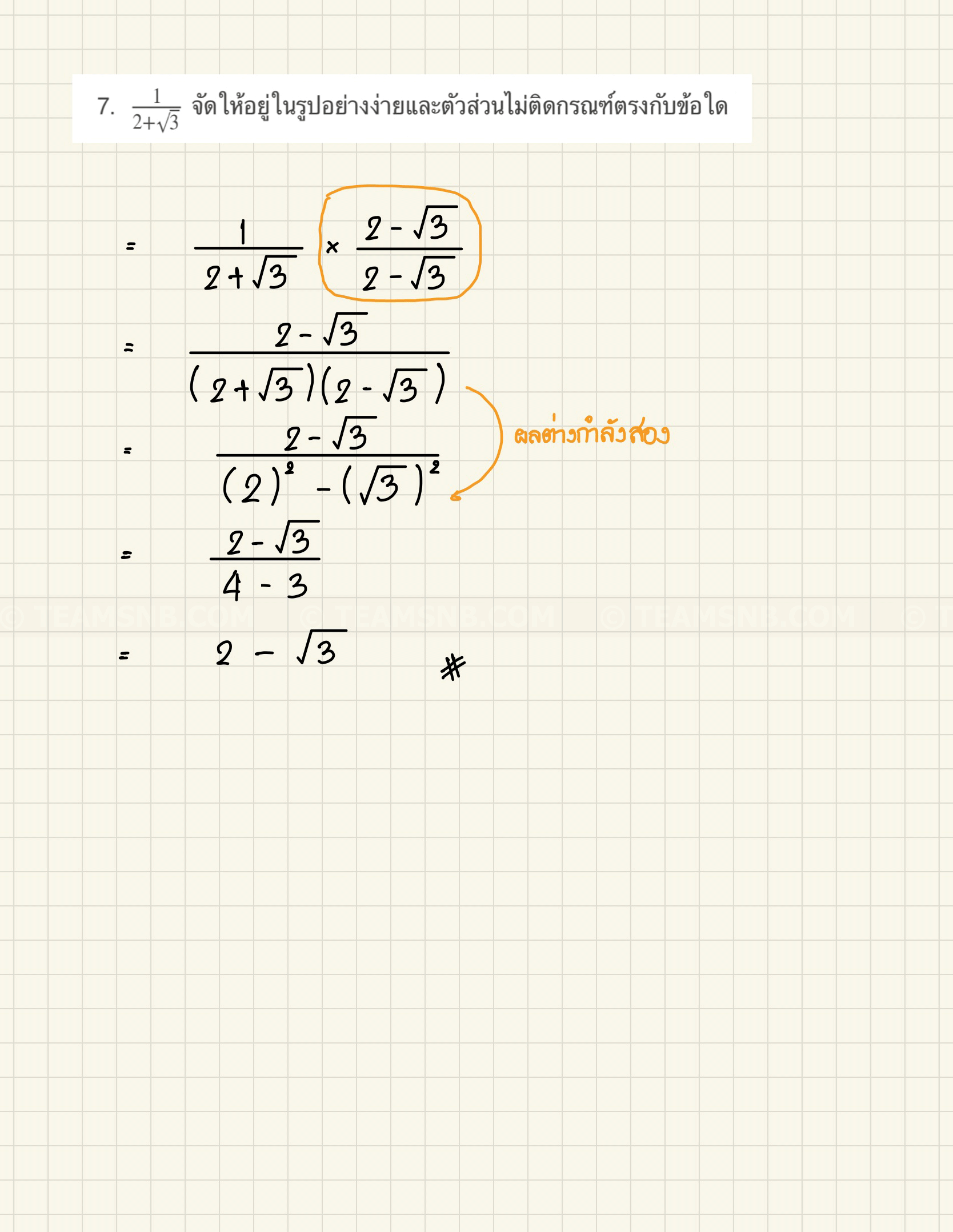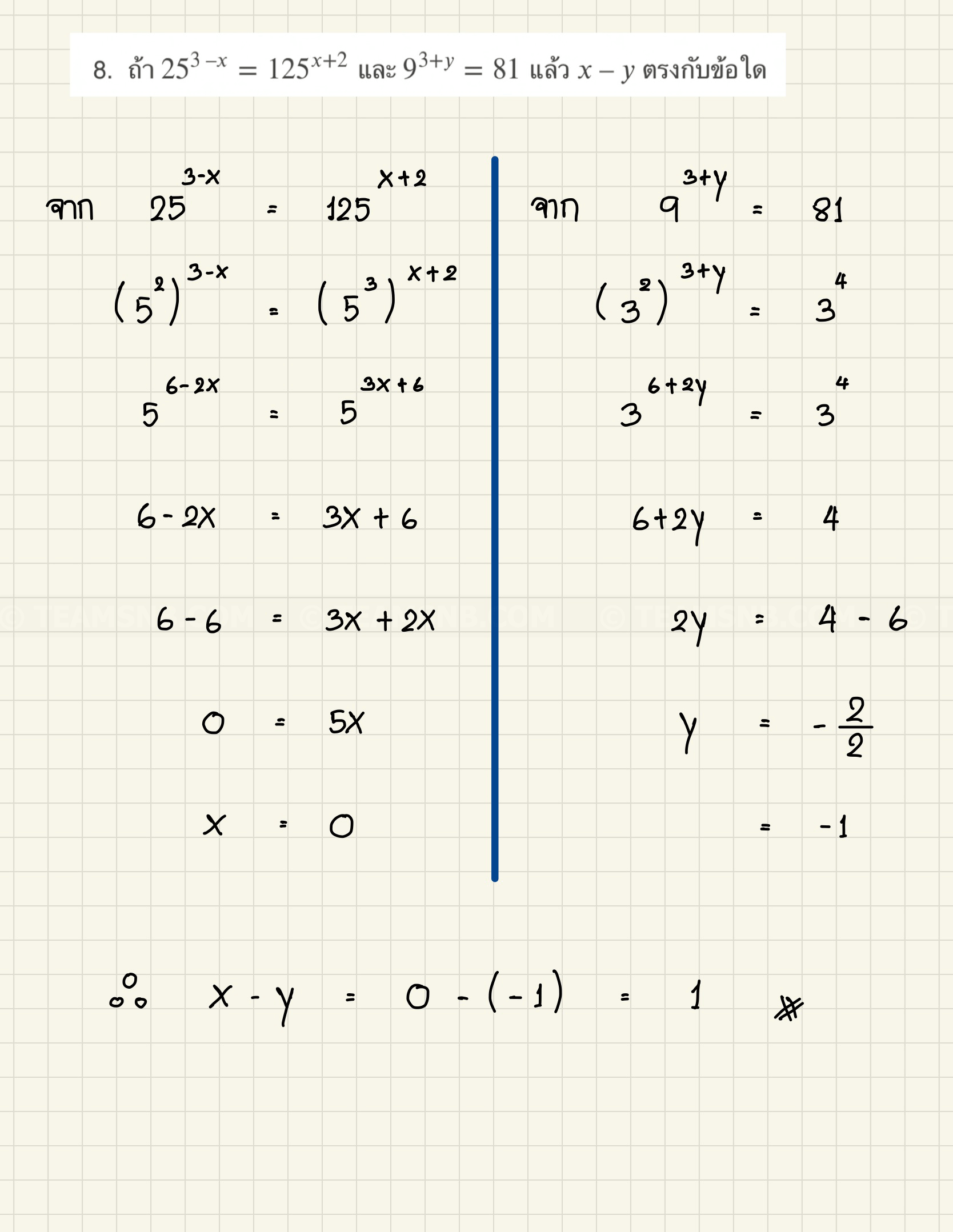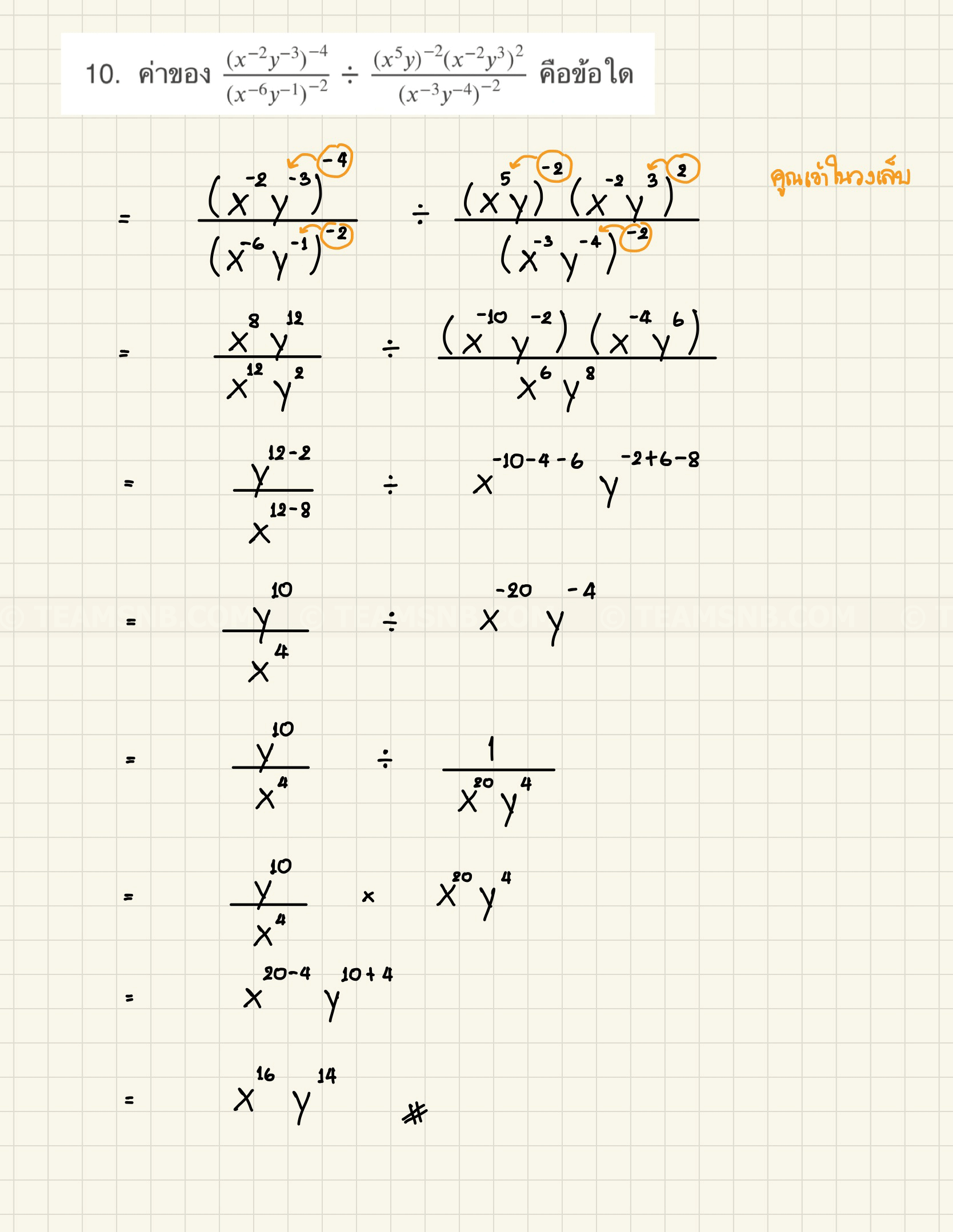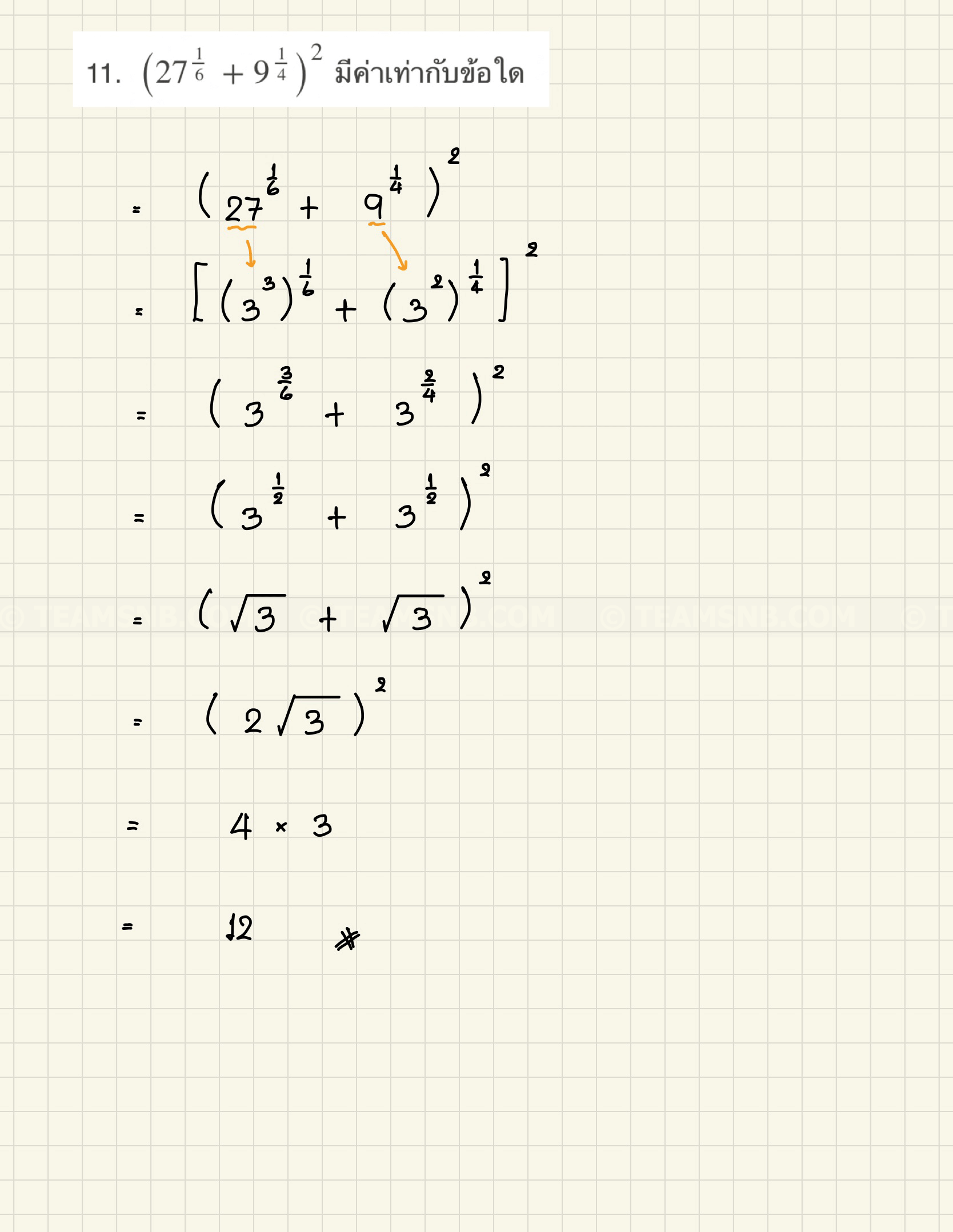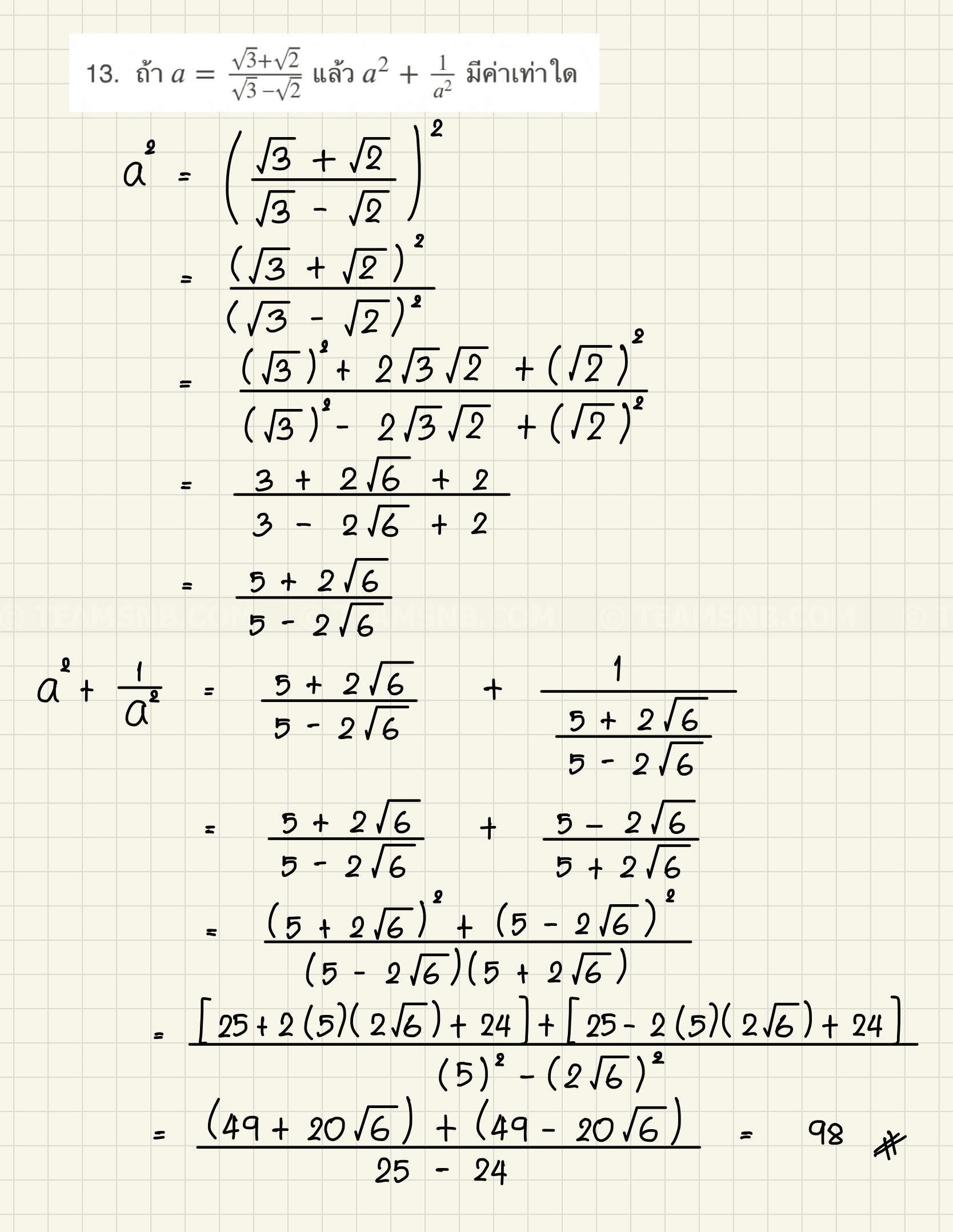Home » High school » แนวข้อสอบกลางภาค คณิตศาสตร์ เรื่อง เลขยกกำลัง
แนวข้อสอบกลางภาค คณิตศาสตร์ เรื่อง เลขยกกำลัง
- \((-3x^2)^4\) มีค่าเท่ากับข้อใด
- \(-81x^6\)
- \(81x^6\)
- \(-81x^8\)
- \(81x^8\)
- ค่าของ \(\sqrt[3]{169} \cdot \sqrt{6} \cdot \sqrt[3]{13} \cdot \sqrt{3} \cdot \sqrt{2} \) เท่ากับข้อใด
- \(19\)
- \(78\)
- \(6\)
- \(36\)
- ถ้า \((\sqrt{2} \ – 1)^x = (\sqrt{2} + 1)^2\) แล้ว \(x + 1\) เท่ากับข้อใด
- \(-1\)
- \(2\)
- \(-2\)
- \(1\)
- ถ้า \(\sqrt{\frac{x}{8}} + \frac{11}{20} = \sqrt[3]{\frac{64}{125}}\) แล้ว \(x\) เท่ากับข้อใด
- \(0.2\)
- \(0.5\)
- \(2\)
- \(4\)
- ถ้า \((a^{-6})^n = a^{-18}\) แล้ว \(n\) เท่ากับข้อใด
- \(-3\)
- \(2\)
- \(-2\)
- \(3\)
- ถ้า \(x\) และ \(y\) เป็นจำนวนจริงซึ่ง \(2^{x^2} = 16\) และ \(-3 \leq y \leq x\) แล้วค่าที่มากที่สุดที่เป็นไปได้ของ \(xy\) เท่ากับข้อใด
- \(2\)
- \(6\)
- \(-6\)
- \(-3\)
- \(\frac{1}{2 + \sqrt{3}}\) จัดให้อยู่ในรูปอย่างง่ายและตัวส่วนไม่ติดกรณฑ์ตรงกับข้อใด
- \(1\)
- \(2 + \sqrt{3}\)
- \(\frac{2 \ – \sqrt{3}}{2}\)
- \(2 \ – \sqrt{3}\)
- ถ้า \(25^{3 \ – x} = 125^{x + 2}\) และ \(9^{3 + y} = 81\) แล้ว \(x \ – y\) ตรงกับข้อใด
- \(0\)
- \(-1\)
- \(2\)
- \(1\)
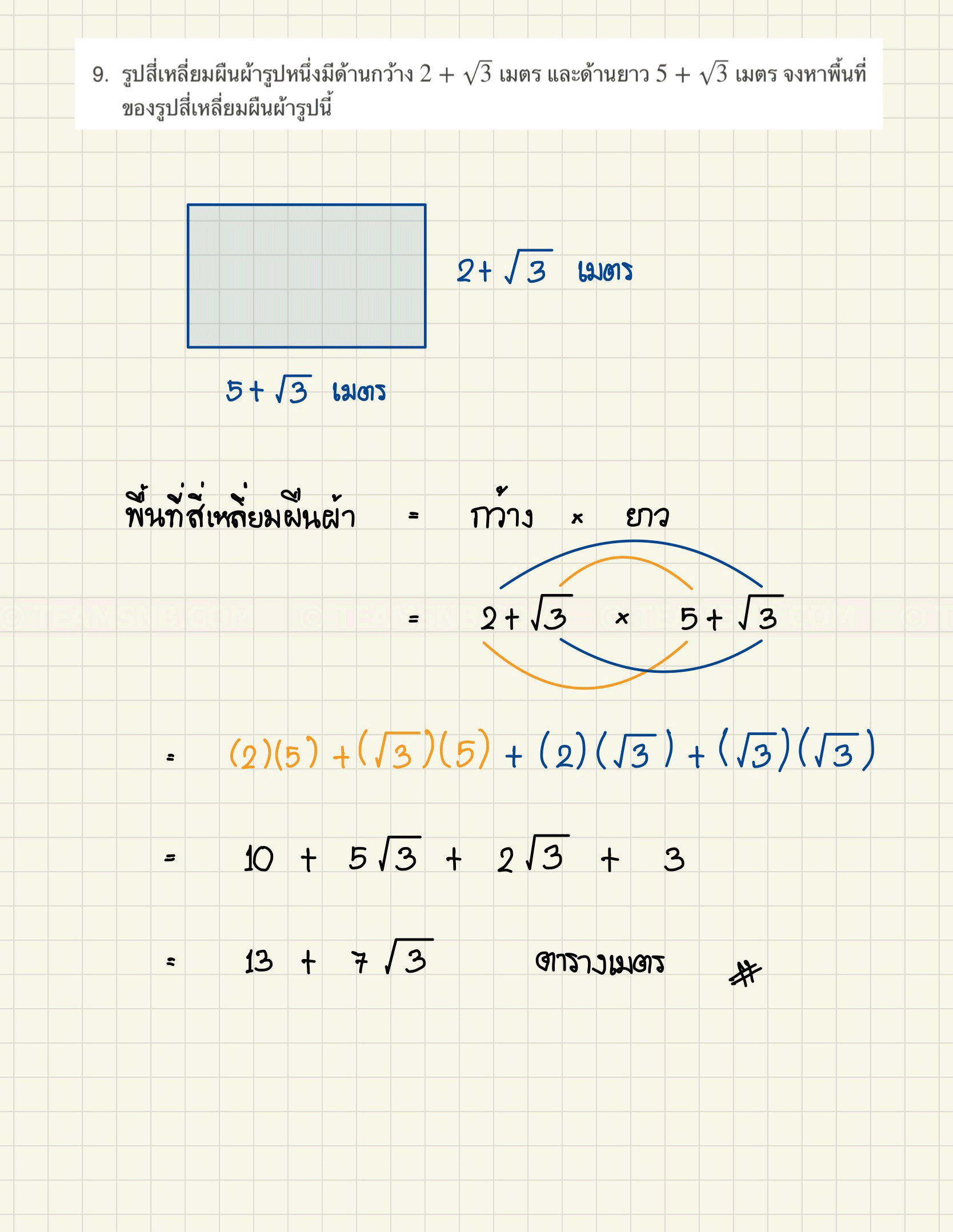
- รูปสี่เหลี่ยมผืนผ้ารูปหนึ่งมีด้านกว้าง \(2 + \sqrt{3}\) เมตร และด้านยาว \(5 + \sqrt{3}\) เมตร จงหาพื้นที่ของรูปสี่เหลี่ยมผืนผ้ารูปนี้
- \(10 + 7\sqrt{3}\)
- \(10 + 8\sqrt{3}\)
- \(13 + 7\sqrt{3}\)
- \(13 + 8\sqrt{3}\)
- ค่าของ \(\frac{(x^{-2}y^{-3})^{-4}}{(x^{-6}y^{-1})^{-2}} \div \frac{(x^5 y)^{-2}(x^{-2}y^{3})^{2}}{(x^{-3}y^{-4})^{-2}}\) คือข้อใด
- \(x^{16}y^{14}\)
- \(\frac{x^{16}}{y^{14}}\)
- \(x^{6}y^{14}\)
- \(\frac{x^{6}}{y^{24}}\)
- \(\big(27^{\frac{1}{6}} + 9^{\frac{1}{4}}\big)^2\) มีค่าเท่ากับข้อใด
- \(3\)
- \(6\)
- \(9\)
- \(12\)
- ข้อใดกล่าวถูกต้อง
- \(a^3 = a \times a \times a \times a\)
- \(a^{\frac{5}{7}} = \sqrt[7]{a^5}\)
- \(a^{\frac{1}{2}} = \sqrt{a} \times \sqrt{a}\)
- \(a^{\frac{1}{3}} = \sqrt[3]{a} \times \sqrt[3]{a} \times \sqrt[3]{a}\)
- ถ้า \(a = \frac{\sqrt{3} + \sqrt{2}}{\sqrt{3} \ – \sqrt{2}}\) แล้ว \(a^2 + \frac{1}{a^2}\) มีค่าเท่าใด
- \(10\)
- \(20\)
- \(49\)
- \(98\)
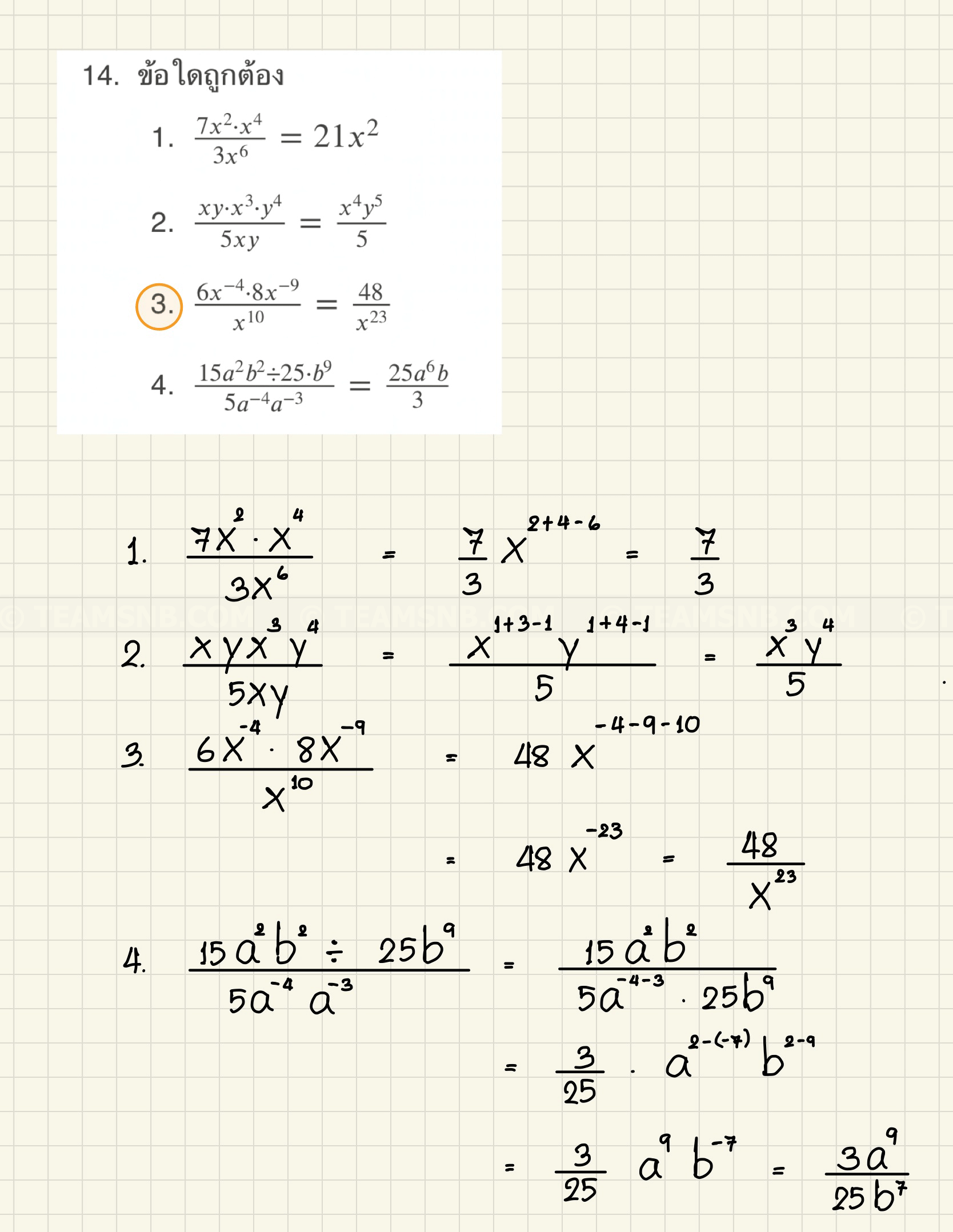
- ข้อใดถูกต้อง
- \(\frac{7x^2 \cdot x^4}{3x^6} = 21x^2\)
- \(\frac{xy \cdot x^3 \cdot y^4}{5xy} = \frac{x^4 y^5}{5}\)
- \(\frac{6x^{-4} \cdot 8x^{-9}}{x^{10}} = \frac{48}{x^{23}}\)
- \(\frac{15a^2 b^2 \div 25 \cdot b^9}{5a^{-4} a^{-3}} = \frac{25a^6 b}{3}\)
- กำหนดให้ \(a = 6^{12} \\ b = 2^9 \times 3^{14} \\ c = 2^{15} \times 3^{10}\) ข้อใดถูกต้อง
- \(c \lt a \lt b\)
- \(c \lt b \lt a\)
- \(a \lt b \lt c\)
- \(b \lt c \lt a\)
- ข้อใดไม่ถูกต้อง
- \(a^0 = a\)
- \(a^{-n} = \frac{1}{a^n}\)
- \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
- \(a^{n} = \frac{1}{a^{-n}}\)
- ค่าของ \(4\sqrt{63} + 5\sqrt{28} \ – 8\sqrt{7}\) มีค่าตรงกับข้อใด
- \(4\sqrt{7}\)
- \(12\sqrt{7}\)
- \(14\sqrt{7}\)
- \(30\sqrt{7}\)
- ข้อใดต่อไปนี้เป็นจริง
ก. รากที่ \(3\) ของ \(-125\) คือ \(-5\)
ข. ถ้า \(\sqrt{40 \ – x^2} = 3x\) แล้ว \(x = 2\) และ \(-2\)
ค. \(\sqrt{x^2} = \left|x\right|\)
- ข้อ ก และ ข ถูก
- ข้อ ก และ ค ถูก
- ข้อ ข และ ค ถูก
- ข้อ ก, ข และ ค ถูก
- \(5a \times 5a \times 5a \times 5a\) เขียนในรูปเลขยกกำลังได้ดังข้อใด
- \(5a^4\)
- \(5^{4a}\)
- \((5a)^4\)
- \(4^{5a}\)
- ผลสำเร็จของ \(\big(8a^5b^3\big)^{\frac{1}{2}} \div \big(4a^2b\big)^{-\frac{1}{2}}\) ตรงกับข้อใด
- \(4a^{\frac{7}{2}}b^2\)
- \(4\sqrt{2}a^{\frac{7}{2}}b^2\)
- \(\sqrt{2}a^{\frac{5}{2}}b^2\)
- \(2a^{\frac{7}{2}}b^2\)