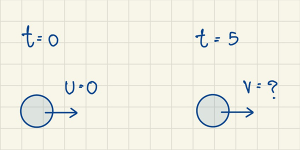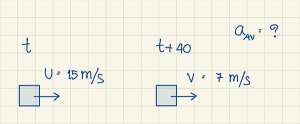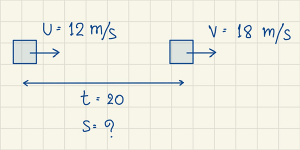Home » High school » แบบฝึกหัด การเคลื่อนที่ในแนวตรง ชุดที่ 1
แบบฝึกหัด การเคลื่อนที่ในแนวตรง ชุดที่ 1
- วัตถุหนึ่งเริ่มเคลื่อนที่จากหยุดนิ่งด้วยความเร่ง 2 m/s2 เมื่อเวลาผ่านไป 5 วินาที จะมีความเร็วเป็นเท่าใด
- รถคันหนึ่งเคลื่อนที่บนถนนตรงด้วยความเร็ว 15 เมตรต่อวินาที หลังจากนั้น 40 วินาที รถยนต์มีความเร็ว 7 เมตรต่อวินาที ในทิศทางเดิม จงหาความเร่งเฉลี่ยของการเคลื่อนที่
- วัตถุชิ้นหนึ่งเคลื่อนที่เป็นเส้นตรงด้วยความเร็วต้น 10 เมตรต่อวินาที โดยมีความเร่ง 5 เมตรต่อ(วินาที)2 ขณะที่วัตถุเคลื่อนที่ได้ระยะทาง 480 เมตร วัตถุเคลื่อนที่มาแล้วกี่วินาที
- วัตถุหนึ่งเคลื่อนที่ในแนวเส้นตรงด้วยความเร็วต้น 5 เมตรต่อวินาที และมีความเร่ง 5 เมตรต่อ(วินาที)2 ขณะที่วัตถุมีความเร็ว 30 เมตรต่อวินาที วัตถุเคลื่อนที่มาได้ระยะทางเท่าใด
- รถยนต์คันหนึ่งวิ่งข้ามสะพานพุทธฯ ขณะที่วิ่งขึ้นสะพานมีความเร็ว 12 เมตรต่อวินาที และเมื่อลงจากสะพานมีความเร็ว 18 เมตรต่อวินาที โดยใช้เวลาวิ่งบนสะพาน 20 วินาที อยากทราบว่าสะพานพุทธยาวเท่าใด
- รถยนต์ A และ B วิ่งเข้าหากันบนถนนตรง รถยนต์ A วิ่งด้วยความเร็ว 10 เมตรต่อวินาที ส่วนรถยนต์ B วิ่งด้วยความเร็ว 20 เมตรต่อวินาที ขณะที่อยู่ห่างกัน 325 รถยนต์ทั้งสองต่างเบรกและหยุดได้พอดีพร้อมกัน โดยอยู่ห่างกัน 25 เมตร เวลาที่ทั้งสองใช้เป็นเท่าไร
- ชูชาติกับชูชีพวิ่งแข่งกันบนถนนตรง โดยชูชาติต่อให้ชูชีพระยะทางค่าหนึ่ง ถ้าทั้งสองคนออกวิ่งพร้อมกันจากจุดหยุดนิ่ง โดยชูชาติวิ่งด้วยความเร่ง 5 เมตรต่อ(วินาที)2 ส่วนชูชาติวิ่งด้วยความเร็ว 4 เมตรต่อ(วินาที)2 ปรากฏว่าชูชาติวิ่งไปทันชูชีพ เมื่อชูชีพวิ่งไปได้ระยะทาง 80 เมตรพอดี อยากทราบว่าชูชาติต่อให้ชูชีพกี่เมตร
- โยนลูกบอลขึ้นในแนวดิ่งจากยอดตึกสูง 160 เมตร ด้วยความเร็วต้น 20 เมตรต่อวินาที จงหา
(ก) ความเร็วของลูกบอลเมื่อเวลาผ่านไป 1, 2 และ 3 วินาที
(ข) ตำแหน่งสูงสุดของลูกบอลจากพื้นดิน
(ค) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกลงถึงที่เดิม
(ง) ตำแหน่งของลูกบอลเมื่อเวลาผ่านไป 5 วินาที
(จ) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกถึงพื้นดิน
- ส้มผลหนึ่งถูกโยนขึ้นไปในแนวดิ่งด้วยความเร็วต้น 10 เมตรต่อวินาที จากพื้นดิน จงหาว่า
(ก) ส้มขึ้นไปได้สูงสุดกี่เมตร
(ข) ส้มใช้เวลานานเท่าใดจึงจะขึ้นถึงจุดสูงสุด
(ค) ส้มใช้เวลานานเท่าใดจึงจะตกถึงที่เดิม นับจากเริ่มโยน
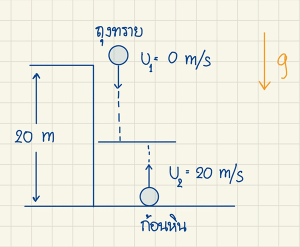
- ปล่อยถุงทรายจากหน้าผาสูง 20 เมตร ขณะเดียวกัน โยนก้อนหินขึ้นไปจากพื้นดินด้วยความเร็วต้น 20 เมตรต่อวินาที จงหาว่า
(ก) นานเท่าใดวัตุทั้งสองจึงสวนกัน
(ข) ขณะสวนกันทั้งคู่มีความเร็วเท่าใด
(ค) ขณะสวนกันทั้งคู่อยู่สูงจากพื้นดินเท่าไร
(ง) หลังจากสวนกันแล้วนานเท่าใดก้อนหินจึงขึ้นถึงจุดสูงสุด
- รถไฟขบวนหนึ่งเริ่มเคลื่อนที่จากจุดหยุดนิ่งจากสถานี ก ไปยังสถานี ข ซึ่งอยู่ห่างกัน 3 กิโลเมตร ใช้เวลา 2 นาที ในเวลา 20 วินาทีแรก รถแล่นด้วยความเร่ง และ 20 วินาทีสุดท้ายรถแล่นด้วยความหน่วง นอกนั้นแล่นด้วยความเร็วคงตัว จงหา
(ก) ความเร่ง
(ข) ความหน่วง
(ค) ความเร็วคงตัว
- บอลลูนหนึ่งลอยขึ้นตรงๆ ด้วยความเร็ว 5 เมตรต่อวินาที เมื่อสูงจากพื้นดิน 30 เมตร ผู้อยู่ในบอลลูนก็ปล่อยถุงทรายลงมาซึ่งตกแบบเสรี นานเท่าใดวัตถุจึงตกถึงพื้น
ดูเฉลยคำตอบ
- วัตถุหนึ่งเริ่มเคลื่อนที่จากหยุดนิ่งด้วยความเร่ง 2 m/s2 เมื่อเวลาผ่านไป 5 วินาที จะมีความเร็วเป็นเท่าใด
วิธีทำ
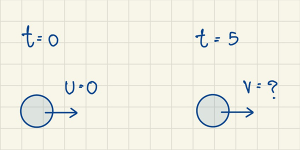
- \(\begin{align*}
v &= u + at \\[6pt]
&= 0 + (2)(5) \\[6pt]
&= 10 \\[6pt]
\therefore v &= 10 \;\; m/s
\end{align*}\)
- รถคันหนึ่งเคลื่อนที่บนถนนตรงด้วยความเร็ว 15 เมตรต่อวินาที หลังจากนั้น 40 วินาที รถยนต์มีความเร็ว 7 เมตรต่อวินาที ในทิศทางเดิม จงหาความเร่งเฉลี่ยของการเคลื่อนที่
วิธีทำ
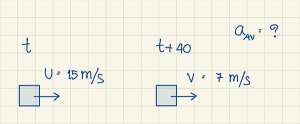
- \(\begin{align*}
v &= u + at \\[6pt]
7 &= 15 + a(40) \\[6pt]
a &= \frac{7 – 15}{40} = \frac{-8}{40} = -\frac{2}{10} \\[6pt]
\therefore a &= -0.2 \;\; m/s^2
\end{align*}\)
- วัตถุชิ้นหนึ่งเคลื่อนที่เป็นเส้นตรงด้วยความเร็วต้น 10 เมตรต่อวินาที โดยมีความเร่ง 5 เมตรต่อ(วินาที)2 ขณะที่วัตถุเคลื่อนที่ได้ระยะทาง 480 เมตร วัตถุเคลื่อนที่มาแล้วกี่วินาที
วิธีทำ
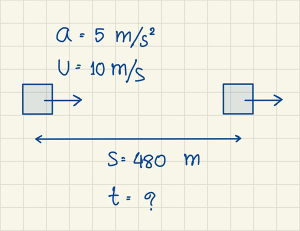
- \(\begin{align*}
s &= ut + \frac{1}{2}at^2 \\[6pt]
480 &= 10t + \frac{1}{2}(5)t^2 \\[6pt]
480 &= 10t + \frac{5}{2}t^2 \\[6pt]
\frac{5}{2}t^2 + 10t \; – 480 &= 0 \\[6pt]
t^2 + 4t \; – 192 &= 0 \\[6pt]
(t + 16)(t – 12) &= 0 \\[6pt]
t &= -16, 12 \\[6pt]
\therefore t &= 12 \;\; s
\end{align*}\)
- วัตถุหนึ่งเคลื่อนที่ในแนวเส้นตรงด้วยความเร็วต้น 5 เมตรต่อวินาที และมีความเร่ง 5 เมตรต่อ(วินาที)2 ขณะที่วัตถุมีความเร็ว 30 เมตรต่อวินาที วัตถุเคลื่อนที่มาได้ระยะทางเท่าใด
วิธีทำ
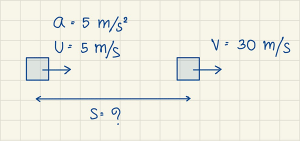
- \(\begin{align*}
v^2 &= u^2 + 2as \\[6pt]
(30)^2 &= 5^2 + 2(5)s \\[6pt]
900 &= 25 + 10s \\[6pt]
875 &= 10s \\[6pt]
s &= 87.5 \\[6pt]
\therefore s &= 87.5 \;\; m
\end{align*}\)
- รถยนต์คันหนึ่งวิ่งข้ามสะพานพุทธฯ ขณะที่วิ่งขึ้นสะพานมีความเร็ว 12 เมตรต่อวินาที และเมื่อลงจากสะพานมีความเร็ว 18 เมตรต่อวินาที โดยใช้เวลาวิ่งบนสะพาน 20 วินาที อยากทราบว่าสะพานพุทธยาวเท่าใด
วิธีทำ
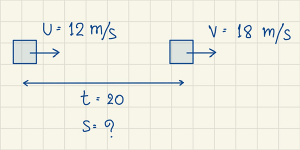
- \(\begin{align*}
s &= \Bigl(\frac{u + v}{2}\Bigl)t \\[6pt]
&= \Bigl(\frac{12 + 18}{2}\Bigl)20 \\[6pt]
&= \bigl(\frac{30}{2}\bigl)20 \\[6pt]
&= 300 \\[6pt]
\therefore s &= 300 \;\; m
\end{align*}\)
- รถยนต์ A และ B วิ่งเข้าหากันบนถนนตรง รถยนต์ A วิ่งด้วยความเร็ว 10 เมตรต่อวินาที ส่วนรถยนต์ B วิ่งด้วยความเร็ว 20 เมตรต่อวินาที ขณะที่อยู่ห่างกัน 325 รถยนต์ทั้งสองต่างเบรกและหยุดได้พอดีพร้อมกัน โดยอยู่ห่างกัน 25 เมตร เวลาที่ทั้งสองใช้เป็นเท่าไร
วิธีทำ
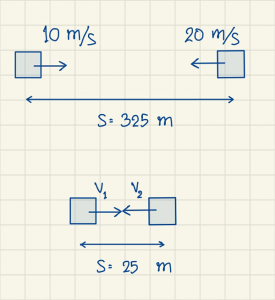
- เมื่อรถทั้งสองหยุดได้พอดีพร้อมกัน แสดงว่า \(v_1 = v_2 = 0\) และรถยนต์ทั้งสองใช้เวลาเท่ากัน
- ให้รถยนต์ A วิ่งได้ระยะทาง \(s_A\) และรถยนต์ B วิ่งได้ระยะทาง \(s_B\) เราจะหาระยะทางที่รถยนต์ทั้งสองวิ่งได้ คือ
- \(\begin{align*}
s_A + s_B &= 325 \; – 25 \\[6pt]
&= 300 \;\; m
\end{align*}\)
- \(\begin{align*}
s_A + s_B &= 300 \\[6pt]
\Bigl(\frac{u_A + v_A}{2}\Bigl)t + \Bigl(\frac{u_B + v_B}{2}\Bigl)t &= 300 \\[6pt]
\Bigl(\frac{10 + 0}{2}\Bigl)t + \Bigl(\frac{20 + 0}{2}\Bigl)t &= 300 \\[6pt]
5t + 10t &= 300 \\[6pt]
15t &= 300 \\[6pt]
t &= 20 \\[6pt]
\therefore t &= 20 \;\; s
\end{align*}\)
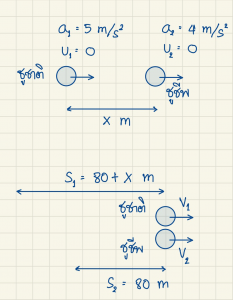
- ชูชาติกับชูชีพวิ่งแข่งกันบนถนนตรง โดยชูชาติต่อให้ชูชีพระยะทางค่าหนึ่ง ถ้าทั้งสองคนออกวิ่งพร้อมกันจากจุดหยุดนิ่ง โดยชูชาติวิ่งด้วยความเร่ง 5 เมตรต่อ(วินาที)2 ส่วนชูชาติวิ่งด้วยความเร็ว 4 เมตรต่อ(วินาที)2 ปรากฏว่าชูชาติวิ่งไปทันชูชีพ เมื่อชูชีพวิ่งไปได้ระยะทาง 80 เมตรพอดี อยากทราบว่าชูชาติต่อให้ชูชีพกี่เมตร
วิธีทำ
- ทั้งสองคนออกวิ่งพร้อมกันจากจุดหยุดนิ่ง แล้ววิ่งไปทันกัน แสดงว่า ทั้งสองคนใช้เวลาวิ่งเท่ากัน โดยจะกำหนดระยะทางที่ชูชาติต่อให้ชูชีพ มีค่าเป็น x เมตร
- เมื่อทั้งสองคนวิ่งไปทันกัน ระยะทางที่ชูชีพวิ่งได้ คือ 80 เมตร และระยะทางที่ชูชาติวิ่งได้ คือ 80 + x เมตร
- เราจะหาเวลาที่ชูชีพวิ่งได้จาก
- \(\begin{align*}
s_2 &= u_2t + \frac{1}{2}a_2t^2 \\[6pt]
80 &= (0)t + \frac{1}{2}(4)t^2 \\[6pt]
80 &= 2t^2 \\[6pt]
t^2 &= 40 \\[6pt]
\end{align*}\)
- พักสมการไว้ก่อน ทีนี้มาดูสมการของชูชาติ
- \(\begin{align*}
s_1 &= u_1t + \frac{1}{2}a_1t^2 \\[6pt]
80 + x &= (0)t + \frac{1}{2}(5)t^2 \\[6pt]
80 + x &= \frac{5}{2}t^2 \\[6pt]
80 + x &= \frac{5}{2}(40) \qquad \text{แทนค่า} \;\; t^2 = 40 \\[6pt]
x &= 100 \; – 80 \\[6pt]
x &= 20 \\[6pt]
\therefore x &= 20 \;\; m
\end{align*}\)
- โยนลูกบอลขึ้นในแนวดิ่งจากยอดตึกสูง 160 เมตร ด้วยความเร็วต้น 20 เมตรต่อวินาที จงหา
(ก) ความเร็วของลูกบอลเมื่อเวลาผ่านไป 1, 2 และ 3 วินาที
(ข) ตำแหน่งสูงสุดของลูกบอลจากพื้นดิน
(ค) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกลงถึงที่เดิม
(ง) ตำแหน่งของลูกบอลเมื่อเวลาผ่านไป 5 วินาที
(จ) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกถึงพื้นดิน
วิธีทำ
- เรากำหนดให้ปริมาณที่มีทิศขึ้นมีค่าเป็นบวก และปริมาณที่มีทิศลงมีค่าเป็นลบ
- โยนลูกบอลขึ้นในแนวดิ่ง \(u = +20 \; m/s\) และ \(g = -10 \; m/s^2\)
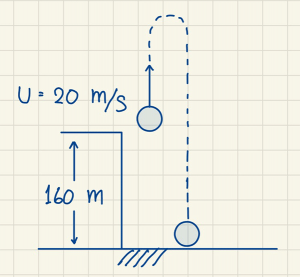
- (ก) ความเร็วของลูกบอลเมื่อเวลาผ่านไป 1, 2 และ 3 วินาที
- \(\begin{align*}
\quad t=1; \qquad v &= u + gt \\[6pt]
&= 20 + (-10)(1) \\[6pt]
&= 20 \; – 10 \\[6pt]
&= 10 \\[10pt]
\quad t=2; \qquad v &= u + gt \\[6pt]
&= 20 + (-10)(2) \\[6pt]
&= 20 \; – 20 \\[6pt]
&= 0 \\[10pt]
\quad t=3; \qquad v &= u + gt \\[6pt]
&= 20 + (-10)(3) \\[6pt]
&= 20 \; – 30 \\[6pt]
&= -10 \\[10pt]
\end{align*}\)
- \(\therefore t=1, \;v = 10 \; m/s\;\) (ลูกบอลกำลังพุ่งขึ้น)
- \(\quad t=2, \;v = 0 \; m/s\;\) (ลูกบอลอยู่จุดสูงสุด และหยุดนิ่ง)
- \(\quad t=3, \;v = -10 \; m/s\;\) (ลูกบอลกำลังตกลงพื้น)
- (ข) ตำแหน่งสูงสุดของลูกบอลจากพื้นดิน หมายถึง ตำแหน่งที่มีอัตราเร็ว = 0
- \(\begin{align*}
\qquad v^2 &= u^2 + 2gs \\[6pt]
0 &= 20^2 + 2(-10)s \\[6pt]
0 &= 400 \; – 20s \\[6pt]
20s &= 400 \\[6pt]
s &= 20 \\[6pt]
\end{align*}\)
- \(\therefore s = 20 \; m\) หรือ ลูกบอลอยู่สูงจากยอดตึก 20 เมตร
- (ค) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกลงถึงที่เดิม หมายถึง ลูกบอลพุ่งขึ้นไปจุดสูงสุด แล้วกำลังตกลงสู่พื้น ในขณะที่มีการกระจัดเป็น 0 เมตร
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
0 &= 20t + \frac{1}{2}(-10)t^2 \\[6pt]
0 &= 20t \; – 5t^2 \\[6pt]
5t^2 \; – 20t &= 0 \\[6pt]
5t(t \;- 4) &= 0 \\[6pt]
t &= 0, 4 \\[6pt]
\end{align*}\)
- \(\therefore t = 4 \; s\) แต่ \(t = 0\) ไม่ใช่คำตอบ เพราะเป็นเวลาที่เราเริ่มโยนลูกบอล
- (ง) ตำแหน่งของลูกบอลเมื่อเวลาผ่านไป 5 วินาที
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
&= 20(5) + \frac{1}{2}(-10)(5)^2 \\[6pt]
&= 100 \; – 5(25) \\[6pt]
&= 100 \; – 125 \\[6pt]
&= -25 \\[6pt]
\end{align*}\)
- \(\therefore s = -25 \; s\;\) (ลูกบอลอยู่ต่ำกว่าจุดที่โยน 25 เมตร)
- (จ) เวลาตั้งแต่เริ่มโยนจนลูกบอลตกถึงพื้นดิน
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
-160 &= 20t + \frac{1}{2}(-10)t^2 \\[6pt]
-160 &= 20t \; – 5(t)^2 \\[6pt]
5t^2 \; – 20t \;- 160 &= 0 \\[6pt]
t^2 \; – 4t \; – 32 &= 0 \\[6pt]
(t \; – 8)(t + 4) &= 0 \\[6pt]
t &= 8, -4
\end{align*}\)
- \(\therefore t = 8 \; s\;\)
- ส้มผลหนึ่งถูกโยนขึ้นไปในแนวดิ่งด้วยความเร็วต้น 10 เมตรต่อวินาที จากพื้นดิน จงหาว่า
(ก) ส้มขึ้นไปได้สูงสุดกี่เมตร
(ข) ส้มใช้เวลานานเท่าใดจึงจะขึ้นถึงจุดสูงสุด
(ค) ส้มใช้เวลานานเท่าใดจึงจะตกถึงที่เดิม นับจากเริ่มโยน
วิธีทำ
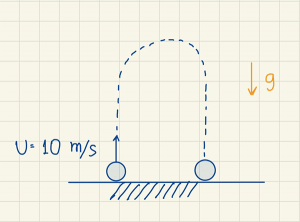
- (ก) ส้มขึ้นไปได้สูงสุดกี่เมตร หมายถึง ให้หาระยะทางเมื่ออัตราเร็วเป็น 0
- \(\begin{align*}
\qquad v^2 &= u^2 + 2gs \\[6pt]
0 &= 10^2 + 2(-10)s \\[6pt]
0 &= 100 \; – 20s \\[6pt]
20s &= 100 \\[6pt]
s &= \frac{100}{20} \\[6pt]
&= 5
\end{align*}\)
- \(\therefore s = 5 \; m\;\)
- (ข) ส้มใช้เวลานานเท่าใดจึงจะขึ้นถึงจุดสูงสุด โดยเราจะเอาระยะทางที่ส้มขึ้นไปได้สูงสุดในข้อ (ก) มาใช้คำนวนหาเวลา
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
5 &= 10t + \frac{1}{2}(-10)t^2 \\[6pt]
5 &= 10t \; – 5t^2 \\[6pt]
5t^2 \; – 10t + 5 &= 0 \\[6pt]
t^2 \; – 2t + 1 &= 0 \\[6pt]
(t \; – 1)(t \;- 1) &= 0 \\[6pt]
t &= 1
\end{align*}\)
- \(\therefore t = 1 \; s\;\)
- (ค) ส้มใช้เวลานานเท่าใดจึงจะตกถึงที่เดิม นับจากเริ่มโยน
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
0 &= 10t + \frac{1}{2}(-10)t^2 \\[6pt]
0 &= 10t \; – 5t^2 \\[6pt]
5t^2 \; – 10t &= 0 \\[6pt]
5t(t \; – 2) &= 0 \\[6pt]
t &= 0, 2
\end{align*}\)
- \(\therefore t = 2 \; s\;\)
- ปล่อยถุงทรายจากหน้าผาสูง 20 เมตร ขณะเดียวกัน โยนก้อนหินขึ้นไปจากพื้นดินด้วยความเร็วต้น 20 เมตรต่อวินาที จงหาว่า
(ก) นานเท่าใดวัตุทั้งสองจึงสวนกัน
(ข) ขณะสวนกันทั้งคู่มีความเร็วเท่าใด
(ค) ขณะสวนกันทั้งคู่อยู่สูงจากพื้นดินเท่าไร
(ง) หลังจากสวนกันแล้วนานเท่าใดก้อนหินจึงขึ้นถึงจุดสูงสุด
วิธีทำ
- (ก) นานเท่าใดวัตุทั้งสองจึงสวนกัน
- เนื่องจาก เราไม่รู้ว่าวัตถุทั้งสองใช้เวลาเท่าไร หรือเคลื่อนที่เป็นระยะทางเท่าไรถึงจะสวนกัน แต่เรารู้ว่าวัตถุทั้งสองจะสวนกัน ทำให้เรารู้ว่าระยะทางที่วัตถุทั้งสองเคลื่อนที่ได้รวมกันเป็น 20 เมตร สามารถเขียนเป็นสมการได้ว่า \(s_1 + s_2 = 20 \; m\)
- คิดที่ถุงทราย ในสมการนี้เราต้องการให้ระยะทางที่ถุงทรายเคลื่อนที่เป็น + ดังนั้น เราจะให้ g เป็น +
- \(\begin{align*}
\qquad s_1 &= ut + \frac{1}{2}gt^2 \\[6pt]
s_1 &= 0 + \frac{1}{2}(10)t^2 \\[6pt]
s_1 &= 5t^2 \qquad \qquad \qquad (1)
\end{align*}\)
- คิดที่ก้อนหิน (คิดตามปกติ โดยให้ทิศขึ้นมีค่าเป็นบวก, ทิศลงมีค่าเป็นลบ)
- \(\begin{align*}
\qquad s_2 &= ut + \frac{1}{2}gt^2 \\[6pt]
s_2 &= 20t + \frac{1}{2}(-10)t^2 \\[6pt]
s_2 &= 20t \; – 5t^2 \qquad \qquad (2)
\end{align*}\)
- \((1) + (2);\)
- \(\begin{align*}
\qquad s_1 + s_2 &= 20t \\[6pt]
20 &= 20t \\[6pt]
t &= 1
\end{align*}\)
- \(\therefore t = 1 \; s\;\)
- (ข) ขณะสวนกันทั้งคู่มีความเร็วเท่าใด
- คิดที่ถุงทราย
- \(\begin{align*}
\qquad v_1 &= u_1 + g_1t \\[6pt]
&= 0 + (-10)(1) \\[6pt]
&= -10
\end{align*}\)
- \(\therefore v_1 = -10 \; m/s\;\)
- ขณะสวนกัน ถุงทรายกำลังตกลงด้วยความเร็ว 10 เมตรต่อวินาที
- คิดที่ก้อนหิน
- \(\begin{align*}
\qquad v_2 &= u_2 + g_2t \\[6pt]
&= 20 + (-10)(1) \\[6pt]
&= 10
\end{align*}\)
- \(\therefore v_2 = 10 \; m/s\;\)
- ขณะสวนกัน ก้อนหินกำลังพุ่งขึ้นด้วยความเร็ว 10 เมตรต่อวินาที
- (ค) ขณะสวนกันทั้งคู่อยู่สูงจากพื้นดินเท่าไร
- คิดที่ถุงทราย
- \(\begin{align*}
\qquad v_1^2 &= u_1^2 + 2gs_1 \\[6pt]
(-10)^2 &= 0 + 2(-10)s_1 \\[6pt]
100 &= -20s_1 \\[6pt]
s_1 &= -5
\end{align*}\)
- \(\therefore s_1 = -5 \; m\;\)
- ขณะสวนกัน ถุงทรายร่วงลงมาจากจุดที่ปล่อย 5 เมตร หรือ อยู่สูงจากพื้นดิน 15 เมตร
- ดังนั้น ก้อนหินจะอยู่สูงจากพื้นดิน 15 เมตรเช่นกัน
- (ง) หลังจากสวนกันแล้วนานเท่าใดก้อนหินจึงขึ้นถึงจุดสูงสุด
- \(\begin{align*}
\qquad v_2 &= u_2 + gt \\[6pt]
0 &= 20 + (-10)t \\[6pt]
10t &= 20 \\[6pt]
t &= 2
\end{align*}\)
- \(\therefore t = 2 \; – 1 = 1 \; s\;\)
- ก้อนหินใช้เวลาตั้งแต่เริ่มโยนจนขึ้นไปถึงจุดสูงสุด 2 วินาที ดังนั้น หลังจากที่สวนกันแล้ว ก้อนหินจะใช้เวลา 1 วินาทีเพื่อขึ้นไปถึงจุดสูงสุด
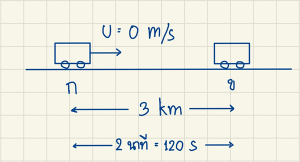
- รถไฟขบวนหนึ่งเริ่มเคลื่อนที่จากจุดหยุดนิ่งจากสถานี ก ไปยังสถานี ข ซึ่งอยู่ห่างกัน 3 กิโลเมตร ใช้เวลา 2 นาที ในเวลา 20 วินาทีแรก รถแล่นด้วยความเร่ง และ 20 วินาทีสุดท้ายรถแล่นด้วยความหน่วง นอกนั้นแล่นด้วยความเร็วคงตัว จงหา
(ก) ความเร่ง
(ข) ความหน่วง
(ค) ความเร็วคงตัว
วิธีทำ
- จากโจทย์ เราทราบว่า สถานี ก และสถานี ข อยู่ห่างกัน 3000 เมตร และ รถไฟใช้เวลาเดินทางรวม 2 นาที หรือ 120 วินาที
- และจากที่โจทย์กำหนด เราสามารถเขียนเป็นกราฟความสัมพันธ์ v-t ได้ดังนี้
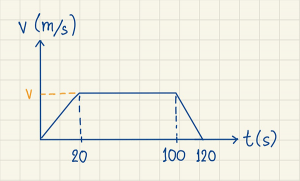
- เราเริ่มจาก หา v ก่อน โดยเรารู้ว่าพื้นที่ใต้กราฟ v-t คือ ระยะทาง ดังนั้น พื้นที่ใต้กราฟทั้งหมด คิดเป็น 3000 คือ พื้นที่ของสามเหลี่ยมทางซ้าย (วินาทีที่ 0-20) + พื้นที่สี่เหลี่ยมผืนผ้าตรงกลาง (วินาทีที่ 20-100) + พื้นที่ของสามเหลี่ยมทางขวา (วินาทีที่ 100-120)
- \(\begin{align*}
\qquad 3000 &= \frac{1}{2}(20)v + (100 – 20)(v) + \frac{1}{2}(20)v \\[6pt]
3000 &= 10v + 80v + 10v \\[6pt]
100v &= 3000 \\[6pt]
v &= 30
\end{align*}\)
- (ก) ความเร่ง
- \(\begin{align*}
\qquad v &= u + at \\[6pt]
30 &= 0 + a(20) \\[6pt]
a &= \frac{30}{20} = 1.5
\end{align*}\)
- \(\therefore a = 1.5 \; m/s^2\;\)
- (ข) ความหน่วง
- \(\begin{align*}
\qquad v &= u + at \\[6pt]
0 &= 30 + a(20) \\[6pt]
a &= -\frac{30}{20} = -1.5
\end{align*}\)
- \(\therefore a = -1.5 \; m/s^2\;\)
- (ค) ความเร็วคงตัว ซึ่งเราได้หาไว้ในตอนแรกแล้ว คือ \(30 \; m/s\)
- บอลลูนหนึ่งลอยขึ้นตรงๆ ด้วยความเร็ว 5 เมตรต่อวินาที เมื่อสูงจากพื้นดิน 30 เมตร ผู้อยู่ในบอลลูนก็ปล่อยถุงทรายลงมาซึ่งตกแบบเสรี นานเท่าใดวัตถุจึงตกถึงพื้น
วิธีทำ
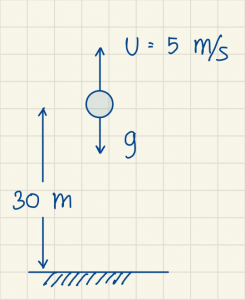
- \(\begin{align*}
\qquad s &= ut + \frac{1}{2}gt^2 \\[6pt]
-30 &= 5t + \frac{1}{2}(-10)t^2 \\[6pt]
-30 &= 5t \; – 5t^2 \\[6pt]
5t^2 \; – 5t \; – 30 &= 0 \\[6pt]
t^2 \; – t \; – 6 &= 0 \\[6pt]
(t \; – 3)(t + 2) &= 0\\[6pt]
t &= 3, -2\\[6pt]
\end{align*}\)
- \(\therefore t = 3 \; s\;\)