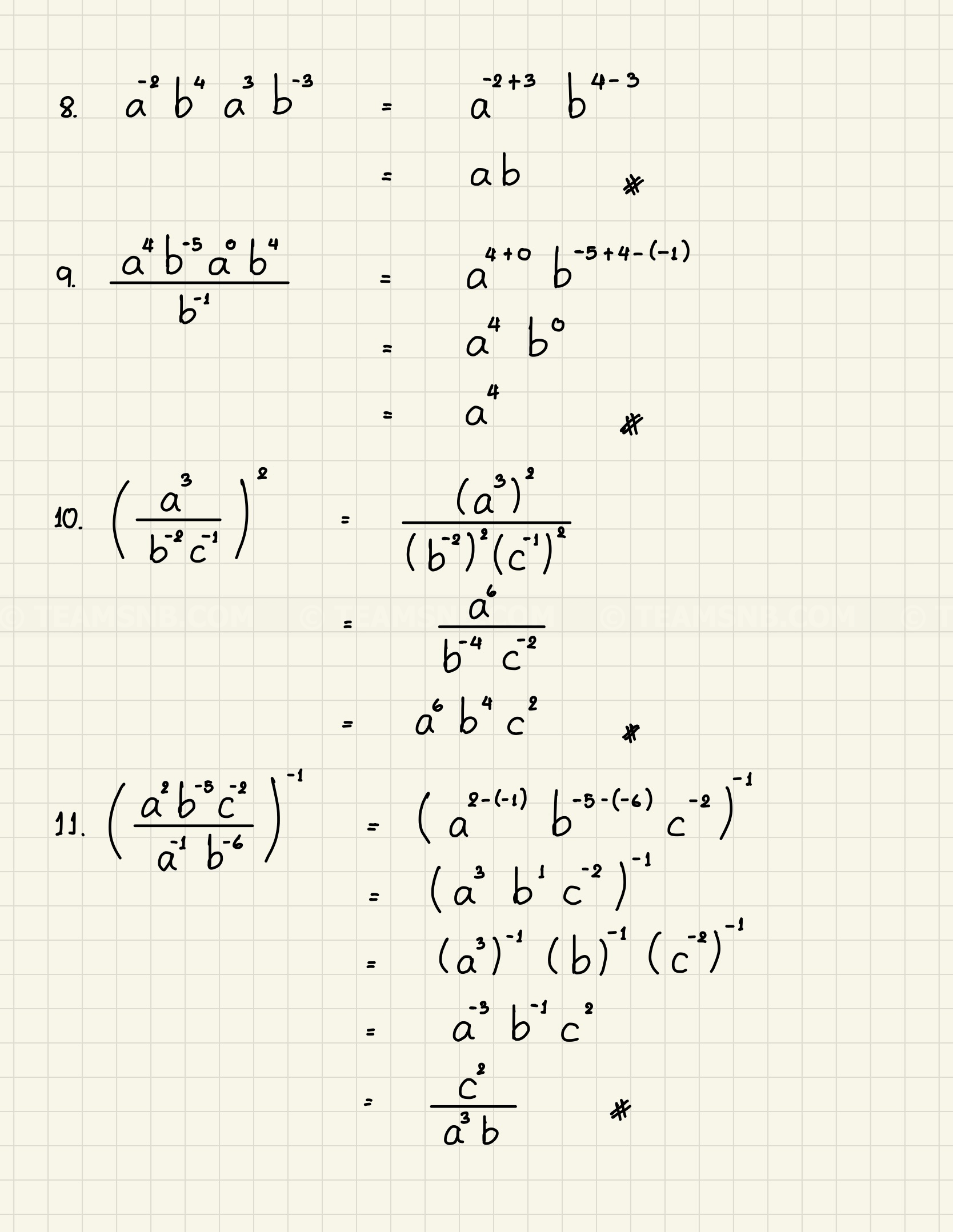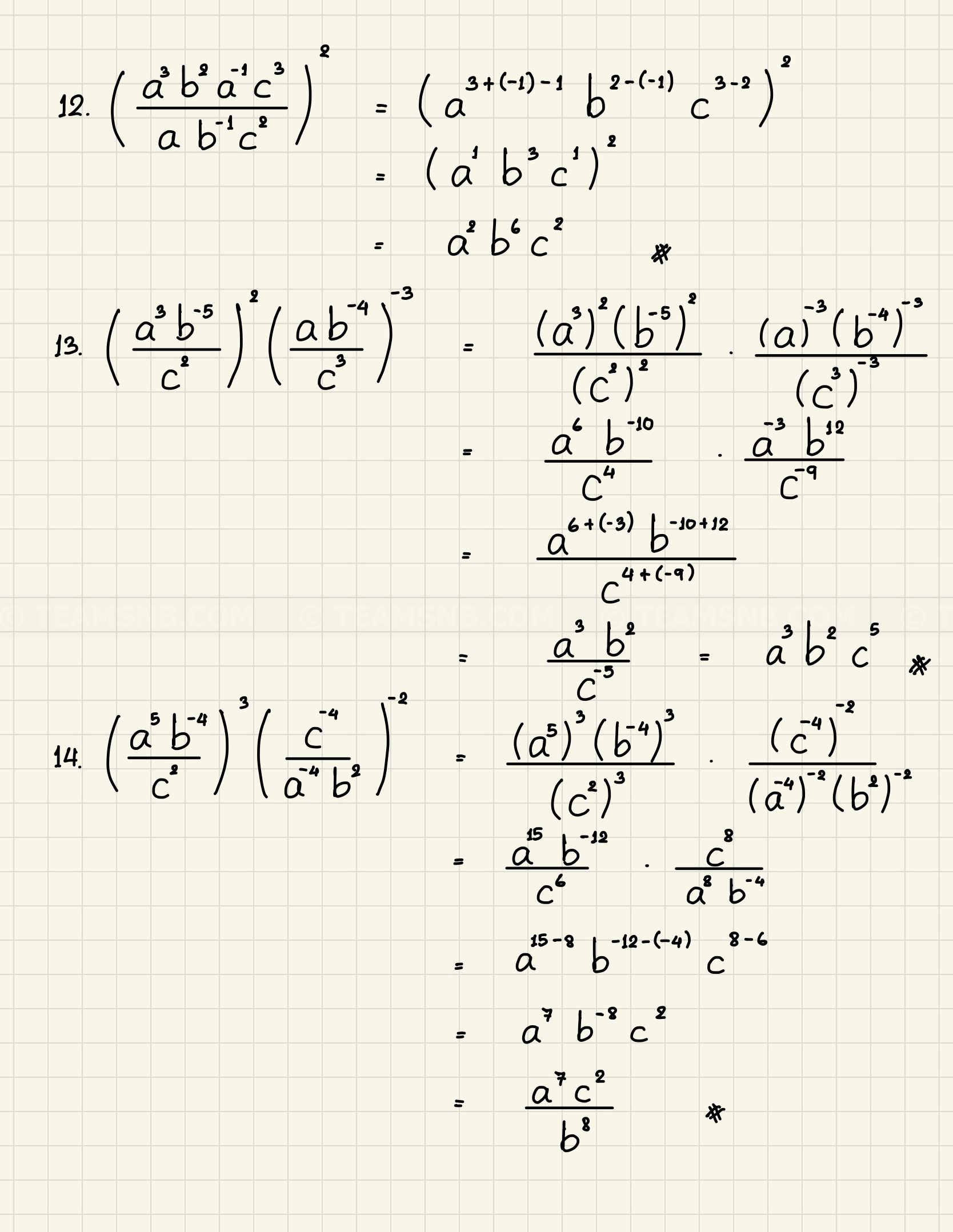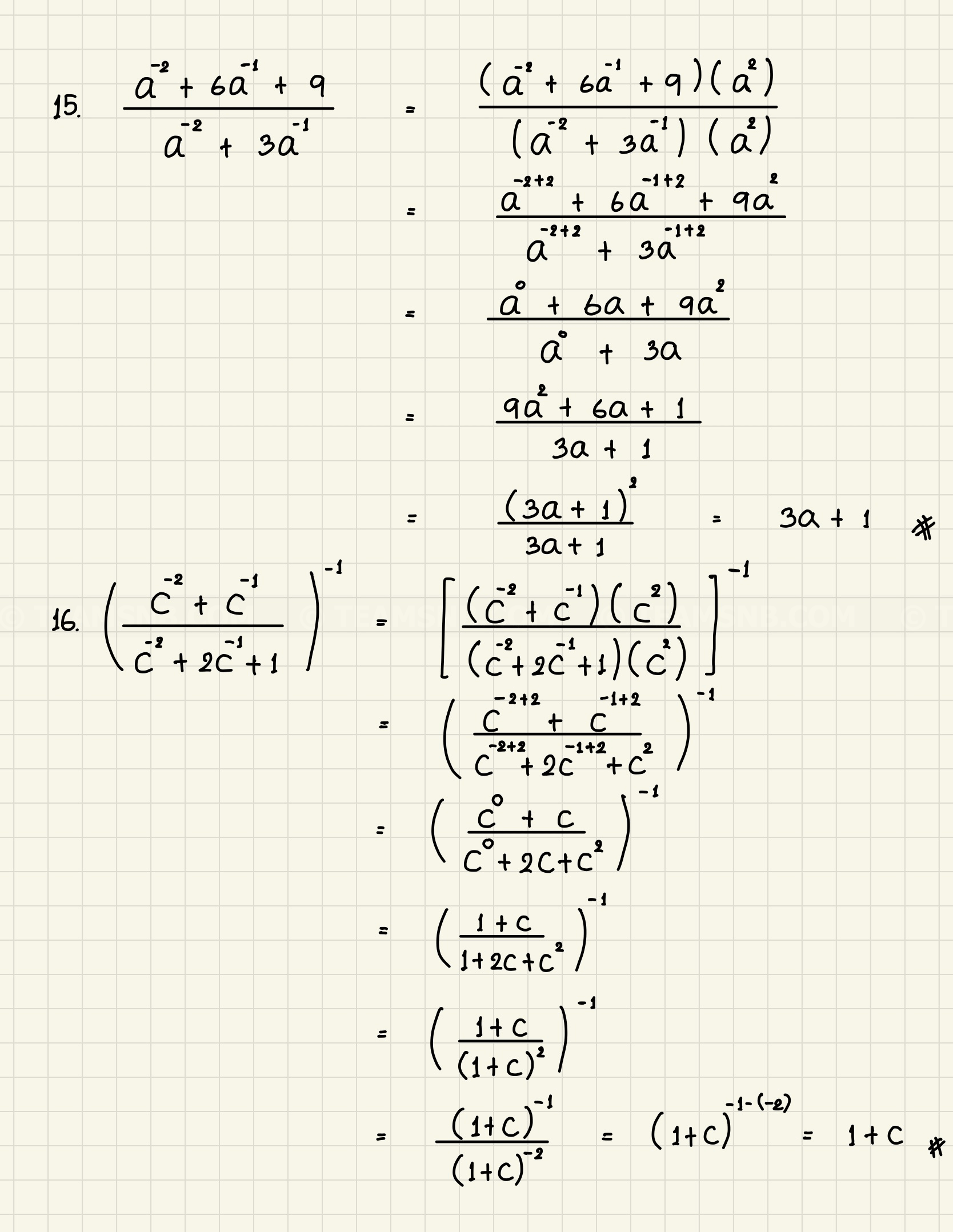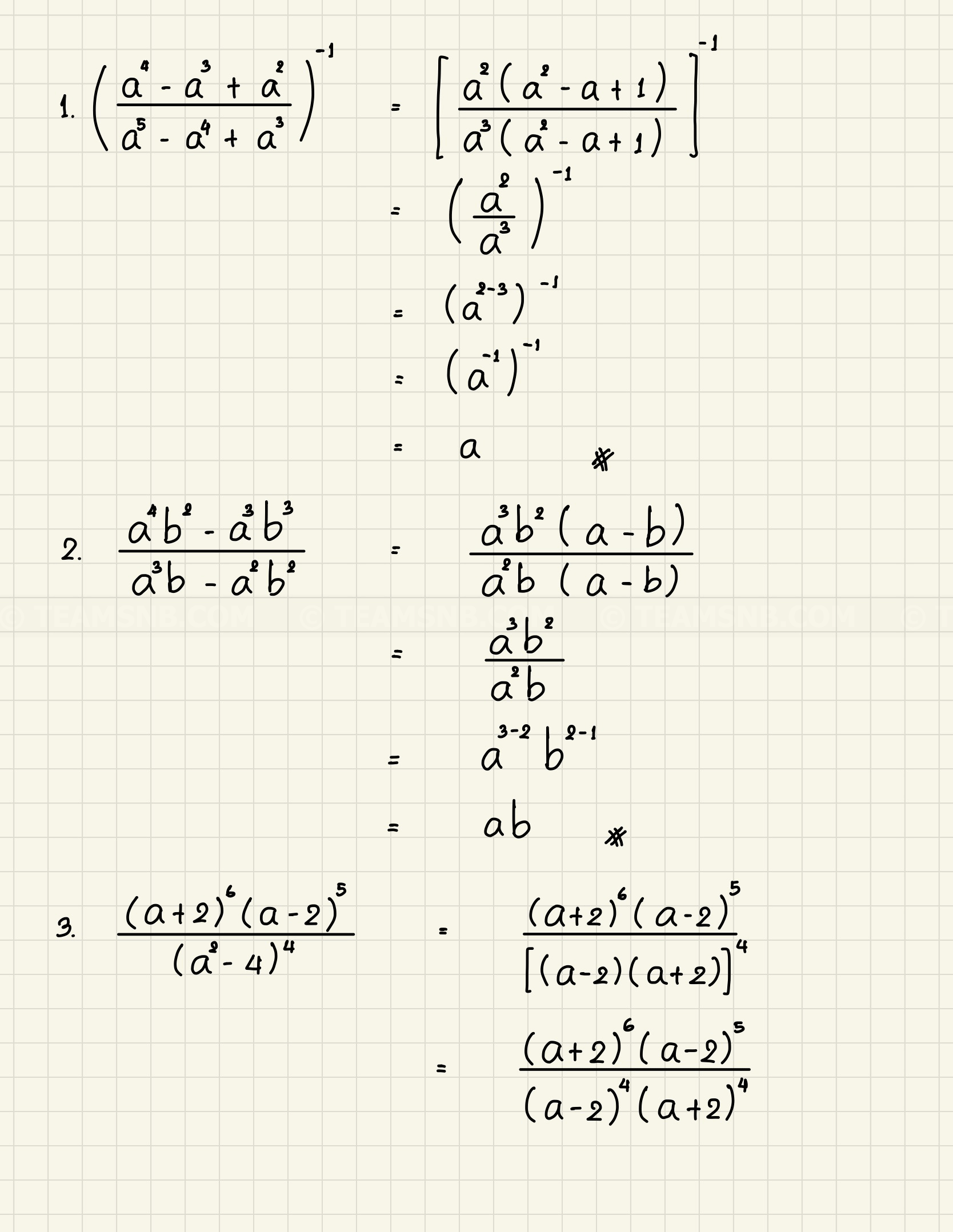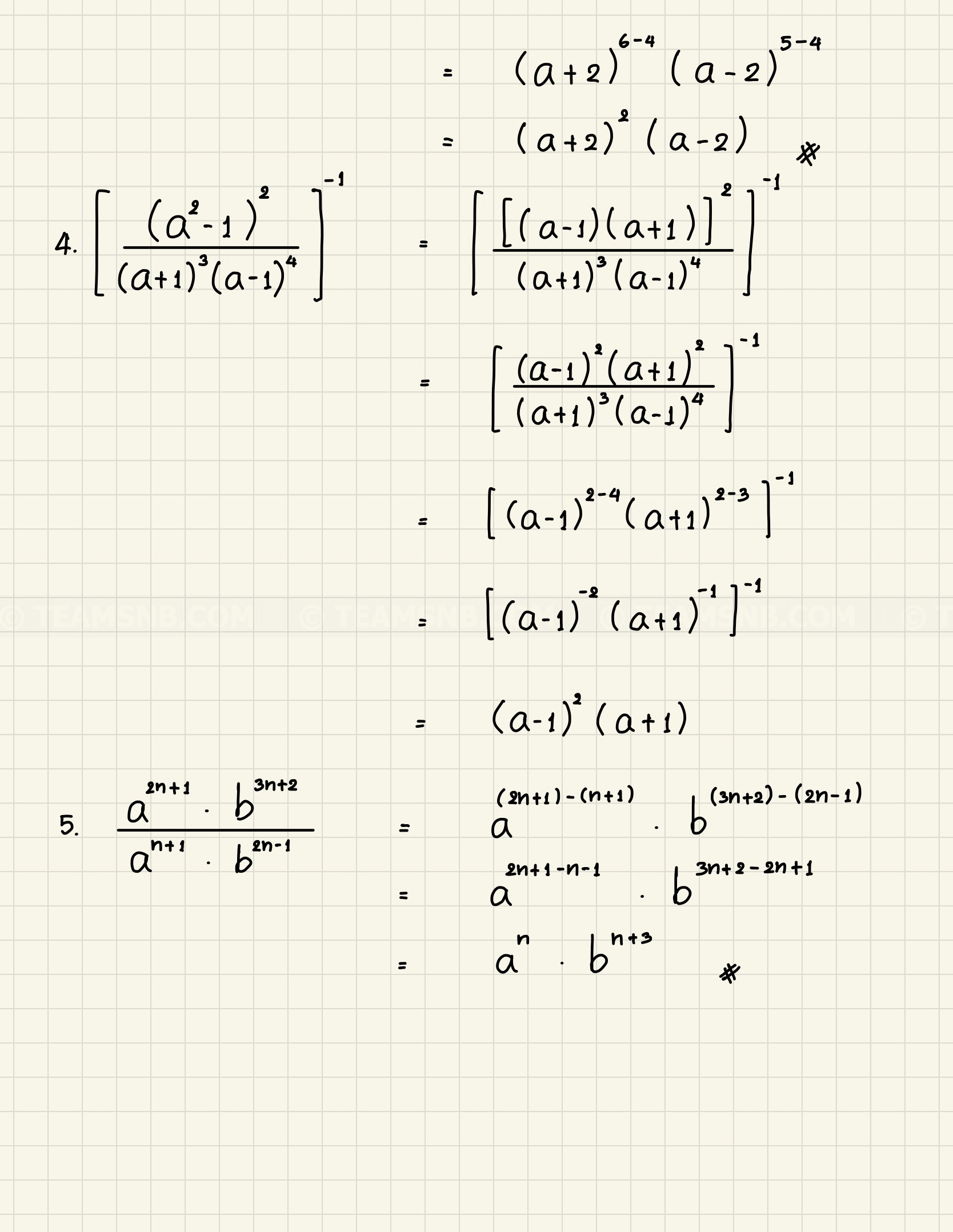สมบัติของเลขยกกำลัง
กำหนด a,b เป็นจำนวนจริงที่ไม่เท่ากับศูนย์ และ m,n เป็นจำนวนเต็ม
am⋅an=am+n(am)n=amn(ab)n=anbn(ab)n=anbnaman=am–nExercise 1.1
1. เขียนจำนวนต่อไปนี้ในรูปอย่างง่าย เมื่อ a,b และ c เป็นจำนวนจริงที่ไม่เท่ากับศูนย์
- 22⋅3−3⋅35
- 23⋅50⋅32⋅2−2
- 23⋅33−2⋅22
- 2−3⋅30⋅5−15−2⋅2−5
- (2−2⋅3⋅5−132⋅2−1)−1
- 9⋅3−223⋅8−1
- 22⋅3−5⋅9442⋅2−4
- a−2b4a3b−3
- a4b−5a0b4b−1
- (a3b−2c−1)2
- (a2b−5c−2a−1b−6)−1
- (a3b2a−1c3ab−1c2)2
- (a3b−5c2)2(ab−4c3)−3
- (a5b−4c2)3(c−4a−4b2)−2
- a−2+6a−1+9a−2+3a−1
- (c−2+c−1c−2+2c−1+1)−1
ดูเฉลยคำตอบ
2. หาค่าของเลขยกกำลังต่อไปนี้
- 23⋅34⋅6−2
- 53⋅3−1153
- 253⋅272⋅15−4
- 816⋅243−827−6
- 16−2⋅83⋅21384⋅32
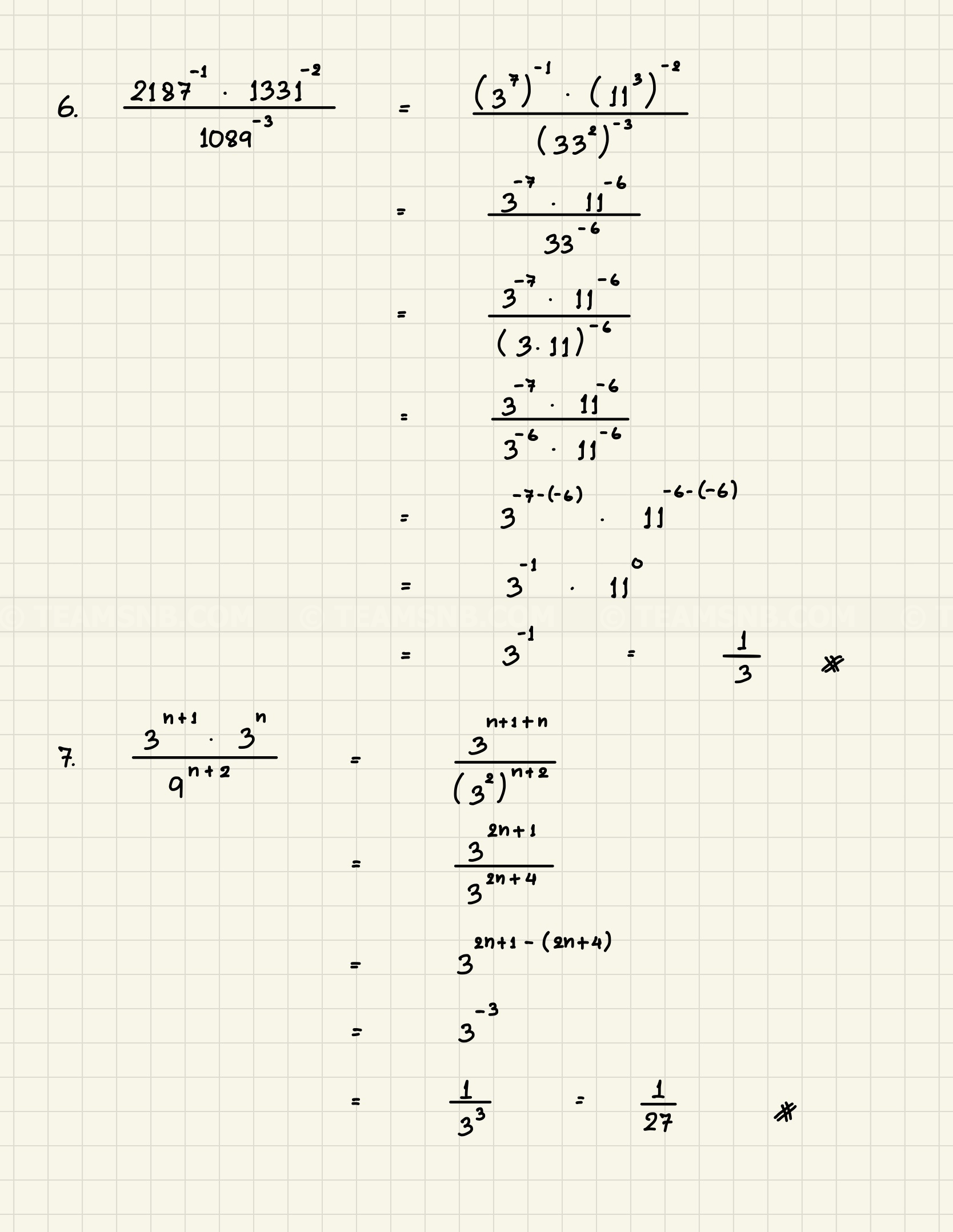
- 2187−1⋅1331−21089−3
- 3n+1⋅3n9n+2
- 2n+3⋅16n−232n−3
ดูเฉลยคำตอบ
3. เขียนจำนวนต่อไปนี้ในรูปอย่างง่าย เมื่อ a,b และ c เป็นจำนวนจริงที่ไม่เท่ากับศูนย์
- (a4–a3+a2a5–a4+a3)−1
- a4b2–a3b3a3b–a2b2
- (a+2)6(a–2)5(a2–4)4
- [(a2–1)2(a+1)3(a–1)4]−1
- a2n+1⋅b3n+2an+1⋅b2n–1
- (a–b)2n+1a−2b3⋅a2b−1c2(a–b)2n–2
ดูเฉลยคำตอบ
